In Young's double slit experiment with monochromatic light of wavelength 600 nm , the distance between the slits is $10^{-3} \mathrm{~m}$. For changing the fringe width by $3 \times 10^{-5} \mathrm{~m}$

a. the screen is moved away from the slit by 5 cm .

b. the screen is moved 5 cm towards the slits.

c. the screen is moved 3 cm towards the slits.

d. the screen is moved away from the slits by 3 cm .

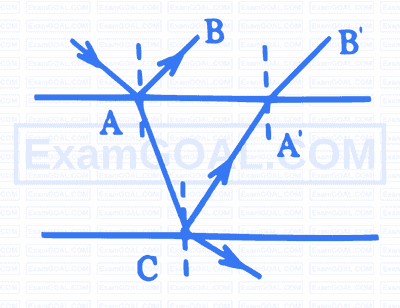
A ray of light of intensity ' I ' is incident on a parallel glass slab at a point ' $A$ ' as shown in figure. It undergoes partial reflection and refraction. At each reflection $25 \%$ of incident energy is reflected. The rays $A B$ and $A B$ undergo interference. The ratio $\frac{\mathrm{I}_{\text {max }}}{\mathrm{I}_{\text {min }}}$ is

In Young's double slit experiment, the distance between screen and aperture is 1 m . The slit width is 2 mm . Light of $6000 \mathop {\rm{A}}\limits^{\rm{o}}$ is used. If a thin glass plate ( $\mu=1.5$ ) of thickness 0.04 mm is placed over one of the slits, then there will be a lateral displacement of the fringes by

In Young's double slit experiment, when light of wavelength 600 nm is used, 18 fringes are observed on the screen. If the wavelength of light is changed to 400 nm , the number of fringes observed on the screen is