An inextensible string of length ' $l$ ' fixed at one end, carries a mass ' $m$ ' at the other end. If the string makes $\frac{1}{\pi}$ revolutions per second around the vertical axis through the fixed end, the tension in the string is [The string makes an angle $\theta$ with the vertical]

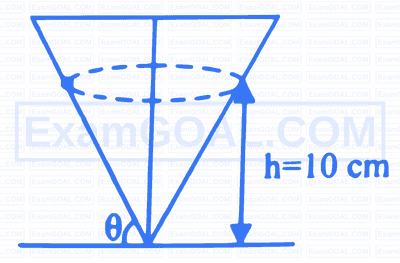
A particle describes a horizontal circle on smooth inner surface of a cone as shown in figure. If the height of the circle above the vertex is 10 cm . The speed of the particle is $\left(\mathrm{g}\right.$, acceleration due to gravity $\left.=10 \mathrm{~m} / \mathrm{s}^2\right)$

Two stones of masses m and 3 m are whirled in horizontal circles, the heavier one in a radius $\left(\frac{\mathrm{r}}{3}\right)$ and lighter one in a radius r . The tangential speed of lighter stone is ' $n$ ' times the value of heavier stone. When the magnitude of centripetal force becomes equal the value of $n$ is

A motor cyclist has to rotate in horizontal circles inside the cylindrical wall of inner radius ' $R$ ' metre. If the coefficient of friction between the wall and the tyres is ' $\mu_{\mathrm{s}}$ ', then the minimum speed required is ( $\mathrm{g}=$ acceleration due to gravity)