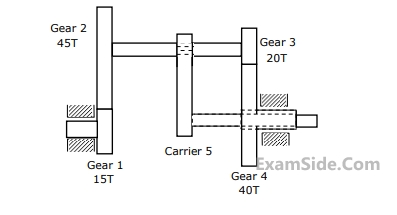
For the epicyclic gear arrangement shown in the figure, $${{\omega _2} = 100}$$ rad/s clockwise (CW) and $${{\omega _{arm}} = 80}$$ rad/s counter clockwise (CCW). The angular velocity $${{\omega _5}}$$ (in rad/s) is

An epicyclic gear train is shown schematically in the adjacent figure The sun gear 2 on the input shaft is a 20 teeth external gear. The planet gear 3 is a 40 teeth external gear. The ring gear 5 is a 100 teeth internal gear. The ring gear 5 is fixed and the gear 2 is rotating at 60 rpm CCW (CCW $$=$$ counter-clockwise and CW $$=$$ clockwise)

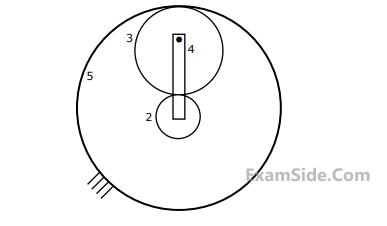
The arm 4 attached to the output shaft will rotate at

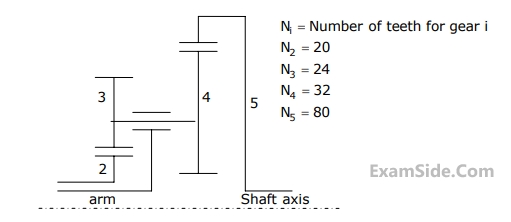
A planetary gear train has four gears and one carrier. Angular velocities of the gears are $${\omega _1},{\omega _2},{\omega _3},$$ and $${\omega _4}$$ respectively. The carrier rotates with angular velocity $${\omega _5}.$$

For $${{\omega _1} = 60}$$ rpm clockwise $$(CW)$$ when looked from the left, what is the angular velocity of the carrier and its direction so that Gear $$4$$ rotates in counter clockwise $$(CCW)$$ direction at twice the angular velocity of Gear $$1$$ when looked from the left?

A planetary gear train has four gears and one carrier. Angular velocities of the gears are $${\omega _1},{\omega _2},{\omega _3},$$ and $${\omega _4}$$ respectively. The carrier rotates with angular velocity $${\omega _5}.$$

What is the relation between the angular velocities of Gear $$1$$ and Gear $$4$$?