
Consider a star of mass m2 kg revolving in a circular orbit around another star of mass m1 kg with m1 \gg m2. The heavier star slowly acquires mass from the lighter star at a constant rate of $\gamma$ kg/s. In this transfer process, there is no other loss of mass. If the separation between the centers of the stars is r, then its relative rate of change $\frac{1}{r}\frac{dr}{dt}$ (in s−1) is given by:

A positive point charge of $10^{-8}$ C is kept at a distance of 20 cm from the center of a neutral conducting sphere of radius 10 cm. The sphere is then grounded and the charge on the sphere is measured. The grounding is then removed and subsequently the point charge is moved by a distance of 10 cm further away from the center of the sphere along the radial direction. Taking $\frac{1}{4\pi\epsilon_0} = 9 \times 10^9$ Nm$^2$/C$^2$ (where $\epsilon_0$ is the permittivity of free space), which of the following statements is/are correct:

Two identical concave mirrors each of focal length f are facing each other as shown in the schematic diagram. The focal length f is much larger than the size of the mirrors. A glass slab of thickness t and refractive index n_0 is kept equidistant from the mirrors and perpendicular to their common principal axis. A monochromatic point light source S is embedded at the center of the slab on the principal axis, as shown in the schematic diagram. For the image to be formed on S itself, which of the following distances between the two mirrors is/are correct:
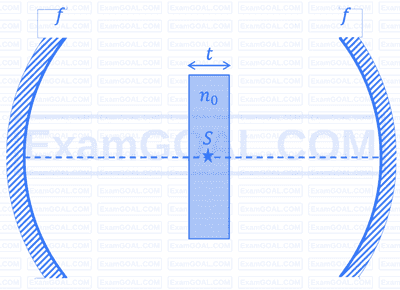

Six infinitely large and thin non-conducting sheets are fixed in configurations I and II. As shown in the figure, the sheets carry uniform surface charge densities which are indicated in terms of $\sigma_0$. The separation between any two consecutive sheets is $1~\mu \text{m}$. The various regions between the sheets are denoted as 1, 2, 3, 4 and 5. If $\sigma_0 = 9~\mu\text{C/m}^2$, then which of the following statements is/are correct:
(Take permittivity of free space $\epsilon_0 = 9 \times 10^{-12}$ F/m)
