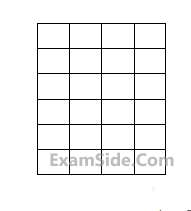
A rectangle with sides of lenght (2m - 1) and (2n - 1) units is divided into squares of unit lenght by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side lengths is

The value of $$$\left( {\matrix{ {30} \cr 0 \cr } } \right)\left( {\matrix{ {30} \cr {10} \cr } } \right) - \left( {\matrix{ {30} \cr 1 \cr } } \right)\left( {\matrix{ {30} \cr {11} \cr } } \right) + \left( {\matrix{ {30} \cr 2 \cr } } \right)\left( {\matrix{ {30} \cr {12} \cr } } \right)....... + \left( {\matrix{ {30} \cr {20} \cr } } \right)\left( {\matrix{ {30} \cr {30} \cr } } \right)$$$
is where $$\left( {\matrix{ n \cr r \cr } } \right) = {}^n{C_r}$$

$$\cos \left( {\alpha - \beta } \right) = 1$$ and $$\,\cos \left( {\alpha + \beta } \right) = 1/e$$ where $$\alpha ,\,\beta \in \left[ { - \pi ,\pi } \right].$$
Paris of $$\alpha ,\,\beta $$ which satisfy both the equations is/are

A simple pendulum has time period T₁. The point of suspension is now moved upward according to the relation y = Kt², (K = 1 m/s²) where y is the vertical displacement. The time period now become T₂. The ratio of $${{T_1^2} \over {T_2^2}}$$ is (g = 10 m/s²)