Consider a base band binary PAM receiver shown below. The additive channel noise $$n(t)$$ is white with power spectral density $${S_N}\left( f \right) = {N_0}/2 = {10^{ - 20}}$$ $$W/Hz$$. The low-pass filter is ideal with unity gain and cut -off frequency $$1MHz$$. Let $${Y_k}$$ represent the random variable $$y\left( {{t_k}} \right)$$.
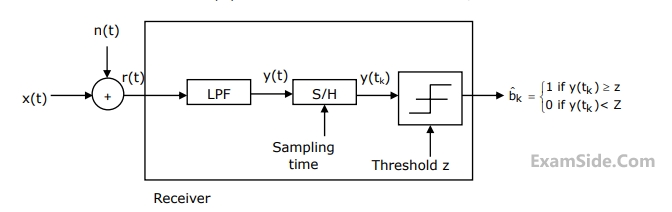
$${Y_k} = {N_k}$$ if transmitted bit $${b_k} = 0$$
$${Y_k} = a + {N_k}$$ if transmitted bit $${b_k} = 1$$
Where $${b_k} = 0$$ represents the noise sample value. The noise sample has a probability density function, $${P_{{N_k}}}\left( n \right)\,\,\,\,\,\,\, = 0.5\alpha {e^{ - \alpha \left| n \right|}}$$ (This has mean zero and variance $$2/{\alpha ^2}$$). Assume transmitted bits to be equiprobable and threshold $$z$$ is set to $$a/2 = {10^{ - 6}}V$$.

The value of the parameter $$\alpha $$( in V^-1 ) is

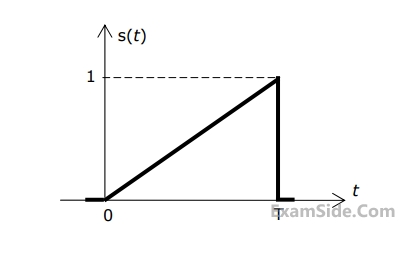
Consider the pulse shape s(t) as shown. The impulse response h(t) of the filter matched to this pulse is

X(t) is a stationary process with the power spectral density S_x(f) > 0 for all f. The process is passed through a system shown below.

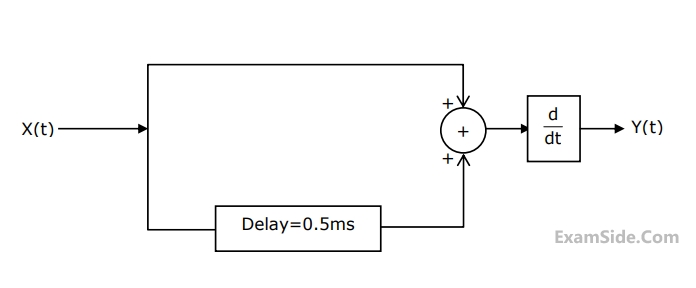
Let S_y(f) be the power spectral density of Y(t). Which one of the following statements is correct?

Consider a base band binary PAM receiver shown below. The additive channel noise $$n(t)$$ is white with power spectral density $${S_N}\left( f \right) = {N_0}/2 = {10^{ - 20}}$$ $$W/Hz$$. The low-pass filter is ideal with unity gain and cut -off frequency $$1MHz$$. Let $${Y_k}$$ represent the random variable $$y\left( {{t_k}} \right)$$.
$${Y_k} = {N_k}$$ if transmitted bit $${b_k} = 0$$
$${Y_k} = a + {N_k}$$ if transmitted bit $${b_k} = 1$$
Where $${b_k} = 0$$ represents the noise sample value. The noise sample has a probability density function, $${P_{{N_k}}}\left( n \right)\,\,\,\,\,\,\, = 0.5\alpha {e^{ - \alpha \left| n \right|}}$$ (This has mean zero and variance $$2/{\alpha ^2}$$). Assume transmitted bits to be equiprobable and threshold $$z$$ is set to $$a/2 = {10^{ - 6}}V$$.

The probability of bit error is