The open loop transfer function of a unity gain negative feedback system is given as

$$G(s) = {1 \over {s(s + 1)}}$$

The Nyquist contour in the s-plane encloses the entire right half plane and a small neighbourhood around the origin in the left half plane, as shown in the figure below. The number of encirclements of the point ($$-$$1 + j0) by the Nyquist plot of G(s), corresponding to the Nyquist contour, is denoted as N. Then N equals to

Consider the following asymptotic Bode magnitude plot ($${\omega \,\,}$$ is in $$rad/s$$)

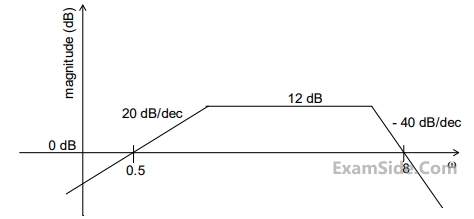
Which one of the following transfer functions is best represented by the above Bode magnitude plot?

Loop transfer function of a feedback system is $$G\left( s \right)H\left( s \right) = {{s + 3} \over {{s^2}\left( {s - 3} \right)}}.$$ Take the Nyquist contour in the clockwise direction. Then, the Nyquist plot of $$G(s)$$ $$H(s)$$ encircles $$-1+j0$$

For the transfer function $$G\left( s \right) = {{5\left( {s + 4} \right)} \over {s\left( {s + 0.25} \right)\left( {{s^2} + 4s + 25} \right)}}.$$ The values of the constant gain term and the highest corner frequency of the Bode plot respectively are