Consider the following asymptotic Bode magnitude plot ($${\omega \,\,}$$ is in $$rad/s$$)

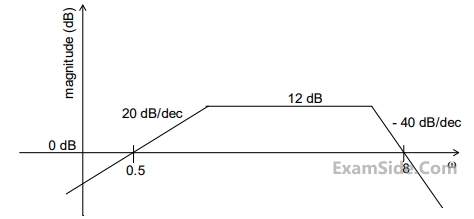
Which one of the following transfer functions is best represented by the above Bode magnitude plot?

Loop transfer function of a feedback system is $$G\left( s \right)H\left( s \right) = {{s + 3} \over {{s^2}\left( {s - 3} \right)}}.$$ Take the Nyquist contour in the clockwise direction. Then, the Nyquist plot of $$G(s)$$ $$H(s)$$ encircles $$-1+j0$$

The magnitude Bode plot of a network is shown in the figure

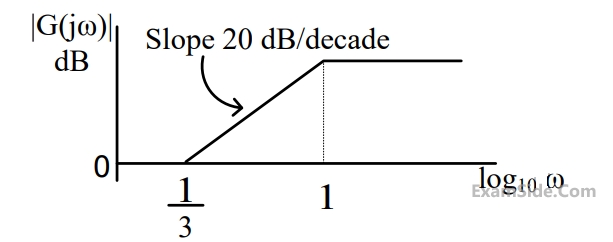
The maximum phase angle $${\phi _m}$$ and the corresponding gain $${G_m}$$ respectively are

For the transfer function $$G\left( s \right) = {{5\left( {s + 4} \right)} \over {s\left( {s + 0.25} \right)\left( {{s^2} + 4s + 25} \right)}}.$$ The values of the constant gain term and the highest corner frequency of the Bode plot respectively are