1
GATE EE 2014 Set 2
MCQ (Single Correct Answer)
+2
-0.6
For the transfer function $$G\left( s \right) = {{5\left( {s + 4} \right)} \over {s\left( {s + 0.25} \right)\left( {{s^2} + 4s + 25} \right)}}.$$ The values of the constant gain term and the highest corner frequency of the Bode plot
respectively are
2
GATE EE 2014 Set 3
MCQ (Single Correct Answer)
+2
-0.6
The magnitude Bode plot of a network is shown in the figure
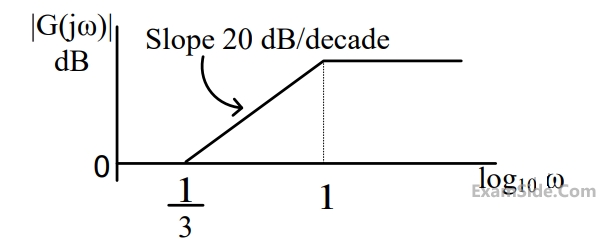

The maximum phase angle $${\phi _m}$$ and the corresponding gain $${G_m}$$ respectively are
3
GATE EE 2014 Set 1
Numerical
+2
-0
The Bode magnitude plot of the transfer function $$G\left( s \right) = {{K\left( {1 + 0.5s} \right)\left( {1 + as} \right)} \over {s\left( {1 + {s \over 8}} \right)\left( {1 + bs} \right)\left( {1 + {s \over {36}}} \right)}}$$ is shown below: Note that $$-6$$ $$dB/octave=-20$$ $$dB/decade.$$ The value of $${a \over {bK}}$$ is _______.
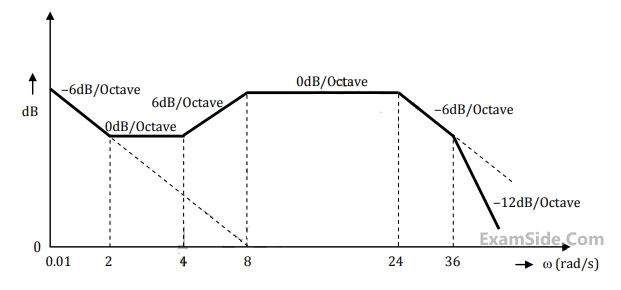

Your input ____
4
GATE EE 2010
MCQ (Single Correct Answer)
+2
-0.6
The frequency response of $$G\left( s \right) = 1/\left[ {s\left( {s + 1} \right)\left( {s + 2} \right)} \right]$$ plotted in the complex $$\,G\left( {j\omega } \right)$$ plane $$\left( {for\,\,0 < \omega < \infty } \right)$$ is
Questions Asked from Polar Nyquist and Bode Plot (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE EE 2024 (2)
GATE EE 2023 (2)
GATE EE 2022 (2)
GATE EE 2016 Set 1 (2)
GATE EE 2014 Set 2 (1)
GATE EE 2014 Set 3 (1)
GATE EE 2014 Set 1 (1)
GATE EE 2010 (1)
GATE EE 2009 (2)
GATE EE 2008 (1)
GATE EE 2007 (1)
GATE EE 2006 (2)
GATE EE 2005 (2)
GATE EE 2004 (2)
GATE EE 2003 (1)
GATE EE 1999 (1)
GATE EE 1997 (1)
GATE EE 1991 (1)
GATE EE Subjects
Electromagnetic Fields
Signals and Systems
Engineering Mathematics
General Aptitude
Power Electronics
Power System Analysis
Analog Electronics
Control Systems
Digital Electronics
Electrical Machines
Electric Circuits



