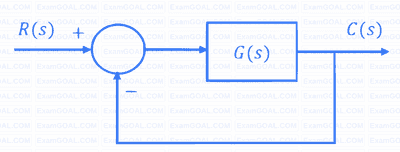
Consider the closed-loop system shown in the figure with $$G(s) = \frac{K(s^2 - 2s + 2)}{(s^2 + 2s + 5)}.$$ The root locus for the closed-loop system is to be drawn for $0 \leq K < \infty$. The angle of departure (between $0^{o}$ and $360^{o})$ of the root locus branch drawn from the pole $(−1 + j2)$, in degrees, is _________________ (rounded off to the nearest integer).

The root locus of the feedback control system having the characteristic equation $${s^2} + 6Ks + 2s + 5 = 0$$ where $$K>0,$$ enters into the real axis at

An open loop transfer function $$G(s)$$ of system is $$G\left( s \right) = {k \over {s\left( {s + 1} \right)\left( {s + 2} \right)}}$$

For a unity feedback system, the breakaway point of the root loci on the real axis occurs at,

The open loop transfer function $$G(s)$$ of a unity feedback control system is given as, $$G\left( s \right) = {{k\left( {s + {2 \over 3}} \right)} \over {{s^2}\left( {s + 2} \right)}}.\,\,$$ From the root locus, it can be inferred that when $$k$$ tends to positive infinity