Consider a unidirectional fluid flow with the velocity field given by

V(𝑥, 𝑦, 𝑧, 𝑡) = 𝑢(𝑥, 𝑡) 𝑖̂

where 𝑢(0,𝑡) = 1. If the spatially homogeneous density field varies with time 𝑡 as

𝜌(𝑡) = 1 + 0.2𝑒^−𝑡

the value of 𝑢(2, 1) is ______________. (Rounded off to two decimal places) Assume all quantities to be dimensionless.

An explosion at time t = 0 releases energy 𝐸 at the origin in a space filled with a gas of density ρ. Subsequently, a hemispherical blast wave propagates radially outwards as shown in the figure.

Let R denote the radius of the front of the hemispherical blast wave. The radius R follows the relationship 𝑅 = 𝑘 𝑡^𝑎 𝐸 ^𝑏 𝜌^𝑐, where k is a dimensionless constant. The value of exponent a is ___________.

(Rounded off to one decimal place)

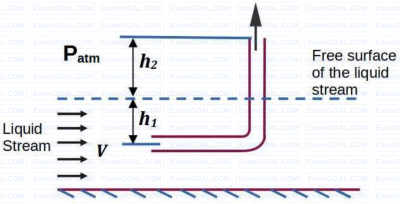
A tube of uniform diameter D is immersed in a steady flowing inviscid liquid stream of velocity V, as shown in the figure. Gravitational acceleration is represented by g. The volume flow rate through the tube is ______.

The steady velocity field in an inviscid fluid of density 1.5 is given to be $\vec{V}=(y^2-x^2)\hat{i}+(2xy)\hat{j} $. Neglecting body forces, the pressure gradient at (x =1, y = 1) is ______.