Consider a lead compensator of the form

$$K(s) = {{1 + {s \over a}} \over {1 + {s \over {\beta a}}}},\beta > 1,a > 0$$

The frequency at which this compensator produces maximum phase lead is 4 rad/s. At this frequency, the gain amplification provided by the controller, assuming asymptotic Bode-magnitude plot of $$K(s)$$, is 6 dB. The values of $$a,\beta$$, respectively, are

An LTI system is shown in the figure where $$G(s) = {{100} \over {{s^2} + 0.1s + 100}}$$. The steady state output of the system, to the input r(t), is given as y(t) = a + b sin(10t + $$\theta$$). The values of a and b will be

The open loop transfer function of a unity gain negative feedback system is given as

$$G(s) = {1 \over {s(s + 1)}}$$

The Nyquist contour in the s-plane encloses the entire right half plane and a small neighbourhood around the origin in the left half plane, as shown in the figure below. The number of encirclements of the point ($$-$$1 + j0) by the Nyquist plot of G(s), corresponding to the Nyquist contour, is denoted as N. Then N equals to

Consider the following asymptotic Bode magnitude plot ($${\omega \,\,}$$ is in $$rad/s$$)

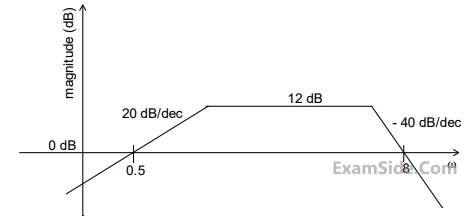
Which one of the following transfer functions is best represented by the above Bode magnitude plot?