In the following network, the voltage magnitudes at all buses are equal to $$1$$ p.u., the voltage phase angles are very small, and the line resistance are negligible. All the line reactances are equal to $$j1\Omega .$$

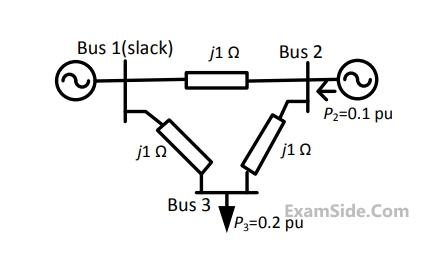
If the base impedance and the line-to-line base voltage are $$100\Omega $$ and $$\,100kV,\,\,$$ respectively, then the real power in MW delivered by the generator connected at the slack bus is

A three–bus network is shown in the figure below indicating the p.u. impedances of each element

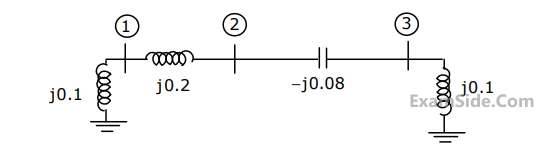
The bus admittance matrix, $$Y$$-$$bus,$$ of the network is

For the $${Y_{bus}}$$ matrix of a $$4$$-bus system given in per unit, the buses having shunt elements are $$${Y_{BUS}} = j\left[ {\matrix{ { - 5} & 2 & {2.5} & 0 \cr 2 & { - 10} & {2.5} & 4 \cr {2.5} & {2.5} & { - 9} & 4 \cr 0 & 4 & 4 & { - 8} \cr } } \right]$$$

The Gauss Seidel load flow method has following disadvantages. Tick the incorrect student.