1
GATE EE 2015 Set 1
MCQ (Single Correct Answer)
+2
-0.6
Determine the correctness or otherwise of the following Assertion (a) and the Reason (R).
Assertion (A): Fast decoupled load flow method gives approximate load flow solution because it uses several assumptions.
Reason (R): Accuracy depends on the power mismatch vector tolerance.
Assertion (A): Fast decoupled load flow method gives approximate load flow solution because it uses several assumptions.
Reason (R): Accuracy depends on the power mismatch vector tolerance.
2
GATE EE 2013
MCQ (Single Correct Answer)
+2
-0.6
For a power system network with $$n$$ nodes, $${Z_{33}}$$ of its bus impedance matrix is $$j0.5$$ per unit. The voltage at mode $$3$$ is $$1.3\angle - {10^0}\,\,$$ per unit. If a capacitor having reactance of $$-j3.5$$ per unit is now added to the network between node $$3$$ and the reference node, the current drawn by the capacitor per unit as
3
GATE EE 2013
MCQ (Single Correct Answer)
+2
-0.6
In the following network, the voltage magnitudes at all buses are equal to $$1$$ p.u., the voltage phase angles are very small, and the line resistance are negligible. All the line reactances are equal to $$j1\Omega .$$
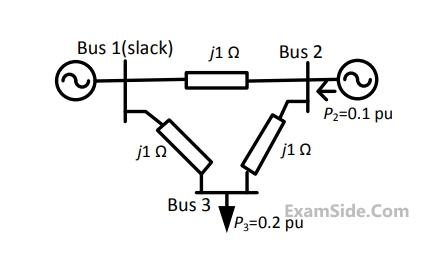

The voltage phase angles in rad at buses $$2$$ and $$3$$ are
4
GATE EE 2013
MCQ (Single Correct Answer)
+2
-0.6
In the following network, the voltage magnitudes at all buses are equal to $$1$$ p.u., the voltage phase angles are very small, and the line resistance are negligible. All the line reactances are equal to $$j1\Omega .$$


If the base impedance and the line-to-line base voltage are $$100\Omega $$ and $$\,100kV,\,\,$$ respectively, then the real power in MW delivered by the generator connected at the slack bus is
Questions Asked from Load Flow Studies (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE EE Subjects
Electromagnetic Fields
Signals and Systems
Engineering Mathematics
General Aptitude
Power Electronics
Power System Analysis
Analog Electronics
Control Systems
Digital Electronics
Electrical Machines
Electric Circuits