Consider the economic dispatch problem for a power plant having two generating units. The fuel costs in $$Rs/MWh$$ along with the generation limits for the two units are given below:
$$\eqalign{ & {C_1}\left( {{P_1}} \right) = 0.01\,P_1^2 + 30{P_1} + 10; \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,100\,MW \le {P_1} \le 150\,MW \cr} $$
$$\eqalign{ & {C_2}\left( {{P_2}} \right) = 0.05\,P_2^2 + 10{P_2} + 10; \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,100\,MW \le {P_2} \le 180\,MW \cr} $$

The incremental cost (in $$Rs/MWh$$) of the power plant when it supplies $$200$$ $$MW$$ is __________.

The fuel cost functions of two power plants are
Plant $${P_1}:\,{C_1} = 0.05\,Pg_1^2 + AP{g_1} + B$$
Plant $${P_2}:\,{C_2} = 0.10\,Pg_2^2 + 3AP{g_2} + 2B$$
Where, $$P{g_1}$$ and $$P{g_2}$$ are the generator powers of two plants and $$A$$ and $$B$$ are the constants. If the two plants optimally share $$1000$$ $$MW$$ load at incremental fuel cost of $$100$$ $$Rs/MWh,$$ the ratio of load shared by plants $${P_1}$$ and $${P_2}$$ is

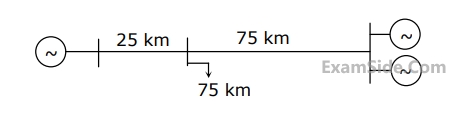
A load center of 120 MW derives power from two power stations connected by 220 kV transmission lines of 25 km and 75 km as shown in the figure below. The three generators G1,G2 and G3 are of 100 MW capacity each and have identical fuel cost characteristics. The minimum loss generation schedule for supplying the 120 MW load is

Three generators are feeding a load of $$100$$ $$MW$$. The details of the generators Rating, Efficiency and Regulation are shown below

In the event of increased load power demand, which of the following will happen?