A 2-bus system and corresponding zero sequence network are shown in the figure.

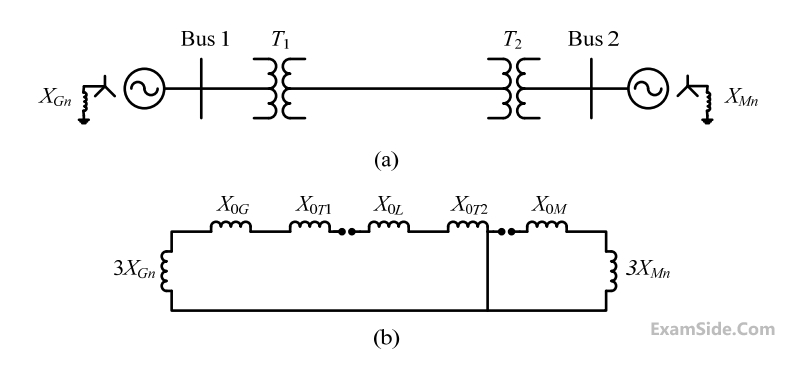
The transformers T₁ and T₂ are connected as

Three phase to ground fault takes place at locations $${F_1}$$ and $${F_2}$$ in the system shown in the figure.

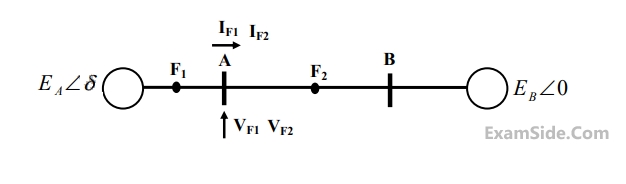
If the fault takes place at location $${F_1}$$, then the voltage and the current at bus A are $${V_F1}$$ and $${{\rm I}_{F1}}$$ respectively. If the fault takes place at location $${F_2}$$, then the voltage and the current at bus A are $${V_{F2}}$$ and $${{\rm I}_{F2}}$$ respectively.

The correct statement about voltages and currents during faults at $${F_1}$$ and $${F_2}$$ is

The sequence components of the fault current are as follows:
$${{\rm I}_{positive}} = j1.5\,pu,\,\,{{\rm I}_{negative}} = - j0.5\,\,pu,$$
$${{\rm I}_{zero}} = - j1\,\,pu.$$ The typeof fault in the system is

A 3-phase transmission line is shown in figure:

Voltage drop across the transmission line is given by the following equation: $$$\left[ {\matrix{ {\Delta {V_a}} \cr {\Delta {V_b}} \cr {\Delta {V_c}} \cr } } \right] = \left[ {\matrix{ {{Z_s}} & {{Z_m}} & {{Z_m}} \cr {{Z_m}} & {{Z_s}} & {{Z_m}} \cr {{Z_m}} & {{Z_m}} & {{Z_s}} \cr } } \right]\left[ {\matrix{ {{i_a}} \cr {{i_b}} \cr {{i_c}} \cr } } \right]$$$
Shunt capacitance of the line can be neglect. If the line has positive sequence impedance of $$15\,\,\Omega $$ and zero sequence in impedance of $$48\,\,\Omega ,$$ then the values of $${{Z_s}}$$ and $${{Z_m}}$$ will be