Match each of the items 1, 2 on the left with the most appropriate item A, B, C or D on the right.

In the case of a linear time invariant system

List - 1
(1) Poles in the right half plane implies.
(2) Impulse response zero for $$t \le 0$$ implies.

List - 2
(A) Exponential decay of output
(B) System is causal
(C) No stored energy in the system
(D) System is unstable

Fig.1, shows the block diagram representation of a control system. The system in block A has an impulse response $${h_A}(t) = {e^{ - t}}\,u(t)$$. The system in block B has an impulse response $${h_B}(t) = {e^{ - 2t}}\,u(t)$$. The block 'k' amplifies its input by a factor k. For the overall system with input x(t) and output y(t)

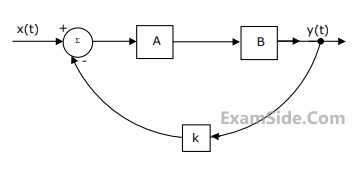
(a) Find the transfer function $${{Y(s)} \over {X(s)}}$$, when k=1

(b) Find the impulse response, when k = 0

(c) Find the value of k for which the system becomes unstable.

$$$\left[ {\matrix{ {Note:u(t)\, \equiv \,0} & {t\, \le \,0} \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \equiv 1} & {t\, > \,0} \cr } } \right]$$$

In Fig. 1, a linear time invariant discrete system is shown. Blocks labeled D represent unit delay elements. For $$n\, < 0,$$ you may assume that $$x\left( n \right),$$ $${y_1}\left( n \right),\,\,{y_2}\left( n \right)$$ are all zero.

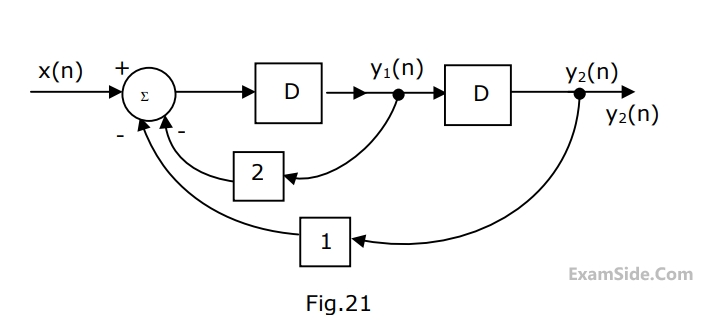
(a) Find the expression for $${y_1}\left( n \right)$$ and $${y_2}\left( n \right)$$ in terms of $$x\left( n \right).$$
(b) Find the transfer function $${y_2}\left( z \right)/X\left( z \right)$$ in the $$z$$-domain.
(c) If $$x\left( n \right) = 1$$ at $$n = 0$$ or $$x\left( n \right) = 0$$ otherwise

Find $${y_2}\left( n \right).$$