ExamSIDE
Questions
PREVIOUS NEXT
1
GATE ME 2014 Set 2
MCQ (Single Correct Answer)
+2
-0.6
The flexural rigidity $$(EI)$$ of a cantilever beam is assumed to be constant over the length of the beam as shown in figure. If a load $$P$$ and bending moment $$PL/2$$ are applied at the free end of the beam then the value of the slope at the free end is GATE ME 2014 Set 2 Strength of Materials - Deflection of Beams Question 11 English
A
$${1 \over 2}$$ $${{P{L^2}} \over {EI}}$$
B
$${{P{L^2}} \over {EI}}$$
C
$${3 \over 2}$$ $${{P{L^2}} \over {EI}}$$
D
$${5 \over 2}$$ $${{P{L^2}} \over {EI}}$$
2
GATE ME 2014 Set 2
MCQ (Single Correct Answer)
+2
-0.6
A cantilever beam of length, $$L,$$ with uniform cross-section and flexural rigidity $$ EI,$$ is loaded uniformly by a vertical load, $$w$$ per unit length. The maximum vertical deflection of the beam is given by
A
$${{w{L^4}} \over {8EI}}$$
B
$${{w{L^4}} \over {16EI}}$$
C
$${{w{L^4}} \over {4EI}}$$
D
$${{w{L^4}} \over {24EI}}$$
3
GATE ME 2014 Set 3
MCQ (Single Correct Answer)
+2
-0.6
A force $$P$$ is applied at a distance $$x$$ from the end of the beam as shown in the figure. What would be the value of $$x$$ so that the displacement at $$'A'$$ is equal to zero? GATE ME 2014 Set 3 Strength of Materials - Deflection of Beams Question 9 English
A
$$0.5L$$
B
$$0.25L$$
C
$$0.33L$$
D
$$0.66L$$
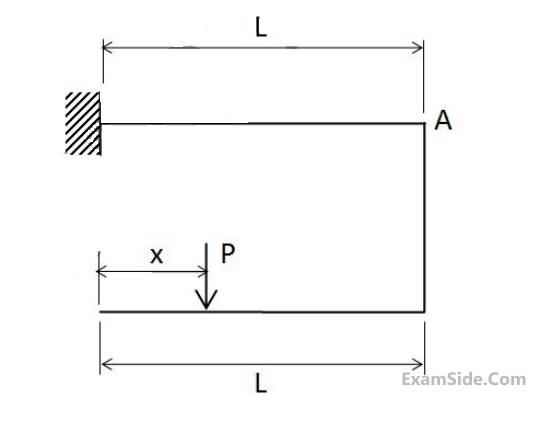
4
GATE ME 2009
MCQ (Single Correct Answer)
+2
-0.6
A triangular-shaped cantilever beam of uniform- thickness is shown in the figure. The young's modulus of the material of the beam is $$E$$. $$A$$ concentrated load $$P$$ is applied at the free end of the beam. GATE ME 2009 Strength of Materials - Deflection of Beams Question 13 English

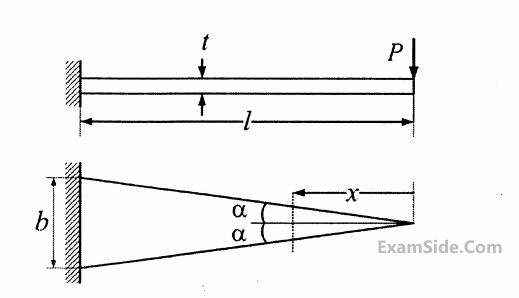
The area moment of inertia of inertia about the neutral axis of a cross-section at a distance $$x$$ measured from the free end is

A
$${{bx{t^3}} \over {6L}}$$
B
$${{bx{t^3}} \over {12L}}$$
C
$${{bx{t^3}} \over {24L}}$$
D
$${{x{t^3}} \over {12}}$$
PREVIOUS NEXT
GATE ME Subjects
Engineering Mechanics
Engineering Mechanics Static and Dynamics
Machine Design
Bolted Riveted and Welded Joints Design For Static Loading Design of Brakes and Clutches Design of Spur Gears Design of Bearings Fatigue Strength
Strength of Materials
Springs Pure Bending Stresses In Beams Simple Stress and Strain Complex Stresses Moment of Inertia Deflection of Beams Shear Force and Bending Moment Torsion Thin Cylinders Columns and Struts Strain Energy Method
Heat Transfer
Conduction Fin Design and Transient Heat Conduction Convection Radiation Heat Exchangers
Production Engineering
Metrology and Inspection Sheet Metal Forming Processes Welding Process Metal Forming Metal Cutting Advance Machine Tools Machining Casting
Industrial Engineering
Queuing Production Planning and Control Line Balancing Forecasting Linear Programming Assignment Pert and Cpm Inventory Control Transportation Scheduling
Turbo Machinery
Turbo Machinery
Theory of Machines
Vibrations Gears and Gear Trains Flywheel Analysis of Plane Mechanisms
Engineering Mathematics
Linear Algebra Vector Calculus Probability and Statistics Differential Equations Transform Theory Calculus Complex Variable Numerical Methods
Fluid Mechanics
Fluid Properties Boundary Layer Turbulent Flow Fluid Dynamics Laminar Flow Fluid Kinematics Fluid Statics
Thermodynamics
Calculation of Work and Heat Entropy and Irreversibility Properties of Pure Substances Basic Concepts and Zeroth Law First Law of Thermodynamics Rankine Cycle Availability Second Law of Thermodynamics
General Aptitude
Verbal Ability Numerical Ability
EXAM MAP
Joint Entrance Examination
JEE MainJEE AdvancedWB JEEBITSAT
Medical
NEET
Graduate Aptitude Test in Engineering
GATE CSEGATE ECEGATE EEGATE MEGATE CEGATE PIGATE IN