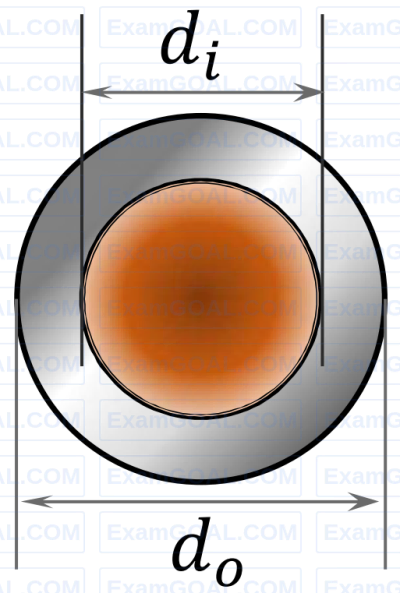
A shaft of length L is made of two materials, one in the inner core and the other in the outer rim, and the two are perfectly joined together (no slip at the interface) along the entire length of the shaft. The diameter of the inner core is d; and the external diameter of the rim is d₀, as shown in the figure. The modulus of rigidity of the core and rim materials are G_i and G₀, respectively. It is given that d₀ = 2d_i and G_i = 3G₀. When the shaft is twisted by application of a torque along the shaft axis, the maximum shear stress developed in the outer rim and the inner core turn out to be τ₀ and τ_i, respectively. All the deformations are in the elastic range and stress-strain relations are linear. Then the ratio τ_i/τ₀ is (round off to 2 decimal places).

A rigid horizontal rod of length $$2L$$ is fixed to a circular cylinder of radius $$R$$ as shown in the figure. Vertical forces of magnitude $$P$$ are applied at the two ends as shown in the figure. The shear modulus for the cylinder is $$G$$ and the Young’s modulus is $$E.$$

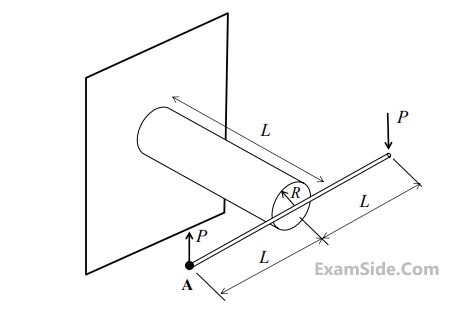
The vertical deflection at point $$A$$ is

Two circular shafts made of same material, one solid $$(S)$$ and one hollow $$(H)$$, have the same length and polar moment of inertia. Both are subjected to same torque. Here. $${\theta _S}$$ is the twist and $${\tau _S}$$ is the maximum shear stress in the solid shaft, whereas $${\theta _H}$$ is the twist and $${\tau _H}$$ is the maximum shear stress in the hollow shaft. Which one of the following is TRUE?

A hollow shaft of $$1$$ m length is designed to transmit a power of $$30$$ kW at $$700$$ rpm. The maximum permissible angle of twist in the shaft is $${1^0}.$$ The inner diameter of the shaft is $$0.7$$ times the outer diameter. The modulus of rigidity is $$80$$ GPa. The outside diameter (in mm) of the shaft is _______