ExamSIDE
Questions
PREVIOUS NEXT
1
GATE ME 2016 Set 2
MCQ (Single Correct Answer)
+2
-0.6
A rigid horizontal rod of length $$2L$$ is fixed to a circular cylinder of radius $$R$$ as shown in the figure. Vertical forces of magnitude $$P$$ are applied at the two ends as shown in the figure. The shear modulus for the cylinder is $$G$$ and the Young’s modulus is $$E.$$ GATE ME 2016 Set 2 Strength of Materials - Torsion Question 6 English

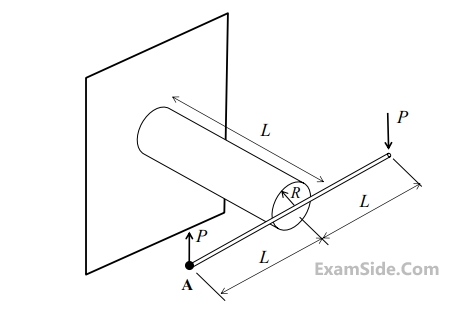
The vertical deflection at point $$A$$ is

A
$$P{L^3}/\left( {\pi {R^4}G} \right)$$
B
$$P{L^3}/\left( {\pi {R^4}E} \right)$$
C
$$2P{L^3}/\left( {\pi {R^4}E} \right)$$
D
$$4P{L^3}/\left( {\pi {R^4}G} \right)$$
2
GATE ME 2015 Set 2
Numerical
+2
-0
A hollow shaft of $$1$$ m length is designed to transmit a power of $$30$$ kW at $$700$$ rpm. The maximum permissible angle of twist in the shaft is $${1^0}.$$ The inner diameter of the shaft is $$0.7$$ times the outer diameter. The modulus of rigidity is $$80$$ GPa. The outside diameter (in mm) of the shaft is _______
Your input ____
3
GATE ME 2012
MCQ (Single Correct Answer)
+2
-0.6
A solid circular shaft needs to be designed to transmit a torque of 50N.m. If the allowable shear stress of the material is $$140$$MPa, assuming a factor of safety of $$2,$$ the minimum allowable design diameter in mm is
A
$$8$$
B
$$16$$
C
$$24$$
D
$$32$$
4
GATE ME 2011
MCQ (Single Correct Answer)
+2
-0.6
A torque $$T$$ is applied at the free end of a stepped rod of circular cross-sections as shown in the figure. The shear modulus of the material of the rod is $$G.$$ The expressions for diameter to produce an angular twist $$\theta $$ at the free end is GATE ME 2011 Strength of Materials - Torsion Question 3 English
A
$${\left( {{{32TL} \over {\pi \theta G}}} \right)^{{1 \over 4}}}$$
B
$${\left( {{{18TL} \over {\pi \theta G}}} \right)^{{1 \over 4}}}$$
C
$${\left( {{{16TL} \over {\pi \theta G}}} \right)^{{1 \over 4}}}$$
D
$${\left( {{{2TL} \over {\pi \theta G}}} \right)^{{1 \over 4}}}$$
PREVIOUS NEXT
GATE ME Subjects
Engineering Mechanics
Engineering Mechanics Static and Dynamics
Machine Design
Bolted Riveted and Welded Joints Design For Static Loading Design of Bearings Design of Brakes and Clutches Design of Spur Gears Fatigue Strength
Strength of Materials
Springs Simple Stress and Strain Complex Stresses Pure Bending Moment of Inertia Shear Force and Bending Moment Stresses In Beams Deflection of Beams Columns and Struts Torsion Strain Energy Method Thin Cylinders
Heat Transfer
Conduction Fin Design and Transient Heat Conduction Convection Radiation Heat Exchangers
Production Engineering
Metrology and Inspection Sheet Metal Forming Processes Welding Process Metal Forming Metal Cutting Advance Machine Tools Machining Casting
Industrial Engineering
Queuing Production Planning and Control Line Balancing Forecasting Linear Programming Assignment Pert and Cpm Inventory Control Transportation Scheduling
Turbo Machinery
Turbo Machinery
Theory of Machines
Analysis of Plane Mechanisms Gears and Gear Trains Vibrations Flywheel
Engineering Mathematics
Linear Algebra Calculus Vector Calculus Probability and Statistics Differential Equations Complex Variable Transform Theory Numerical Methods
Fluid Mechanics
Fluid Properties Boundary Layer Turbulent Flow Fluid Dynamics Laminar Flow Fluid Kinematics Fluid Statics
Thermodynamics
Calculation of Work and Heat Entropy and Irreversibility Properties of Pure Substances Basic Concepts and Zeroth Law First Law of Thermodynamics Rankine Cycle Availability Second Law of Thermodynamics
General Aptitude
Verbal Ability Numerical Ability
EXAM MAP
Joint Entrance Examination
JEE MainJEE AdvancedWB JEEBITSAT
Medical
NEET
Graduate Aptitude Test in Engineering
GATE CSEGATE ECEGATE EEGATE MEGATE CEGATE PIGATE IN