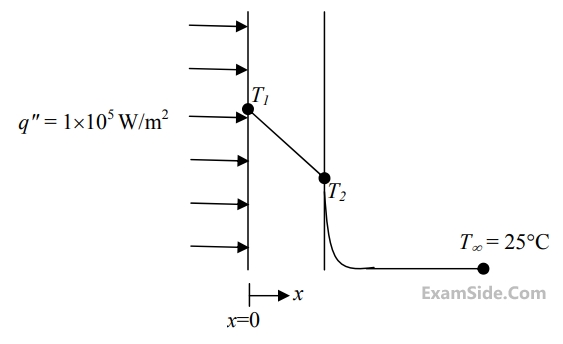
Consider one dimensional steady state heat conduction across a wall (as shown in figure below) of thickness $$30$$ $$mm$$ and thermal conductivity $$15$$ $$W/m.K.$$ At $$x=0,$$ a constant heat flux, $$q'' = 1 \times {10^5}\,\,W/{m^2}$$ is applied. On the other side of the wall, heat is removed from the wall by convection with a fluid at $${25^ \circ }C$$ and heat transfer coefficient of $$250W/{m^2}.K.$$ The temperature (in $${}^ \circ C$$), at $$x=0$$ is ___________

The non-dimensional fluid temperature profile near the surface of a convectively cooled flat plate is given by $${{{T_w} - T} \over {{T_w} - {T_\infty }}} = a + b{y \over L} + c{\left( {{y \over L}} \right)^2},$$ where $$y$$ is measured perpendicular to the plate, $$L$$ is the length, and $$a,b$$ and $$c$$ are arbitrary constants. $${{T_w}}$$ and $${{T_\infty }}$$ are wall and ambiyent temperatures, respectively. If the thermal conductivity of the fluid is $$k$$ and the wall heat flux is $$q'',$$ the Nusselt number $$\,{N_u} = {{q''} \over {{T_w} - {T_\infty }}}{L \over k}$$ is equal to

The ratios of the laminar hydrodynamic boundary layer thickness to thermal boundary layer thickness of flows of two fluids $$P$$ and $$Q$$ on a flat plate are $${1 \over 2}$$ and $$2$$ respectively. The Reynolds number based on the plate length for both the flows is $${10^4}.$$ The Prandtl and Nusselt numbers for $$P$$ are $${1 \over 8}$$ and $$35$$ respectively. The Prandtl and Nusselt number for $$Q$$ are respectively

Match the following

List-$${\rm I}$$
$$P.$$ Compressible flow
$$Q.$$ Free surface flow
$$R.$$ Boundary layer flow
$$S.$$ Pipe flow
$$T.$$ Heat convection

List-$${\rm II}$$
$$U.$$ Renolds number
$$V.$$ Nussult number
$$W.$$ Weber number
$$X.$$ Froude number
$$Y.$$ Mach number
$$Z.$$ Skin friction coefficient