A generator feeds power to an infinite bus through a double circuit transmission line. A $$3$$ phase fault occurs at the middle point of one of the lines. The infinite bus voltage is $$1$$ pu, the transient internal voltage of the generator is $$1.1$$ pu and the equivalent transfer admittance during fault is $$0.8$$ pu. The 100 MVA generator has an inertia constant of $$5$$ MJ/MVA and it was delivering $$1.0$$ pu power prior of the fault with rotor power angle of $${30^ \circ }\,\,$$. The system frequency is 50Hz.

If the initial accelerating power is $$X$$ pu, the initial acceleration in elect deg/sec², and the inertia constant in MJ-sec/elect deg respectively will be

A generator feeds power to an infinite bus through a double circuit transmission line. A 3 phase fault occurs at the middle point of one of the lines. The infinite bus voltage is 1 pu, the transient internal voltage of the generator is 1.1 pu and the equivalent transfer admittance during fault is 0.8 pu. The 100 MVA generator has an inertia constant of $$5$$ MJ/MVA and it was delivering 1.0 pu power prior of the fault with rotor power angle of $${30^ \circ }\,\,$$. The system frequency is 50Hz.

The initial accelerating power (in pu) will be

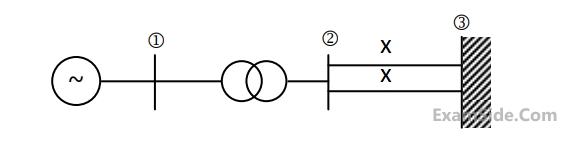
A generator with constant 1.0 p.u. terminal voltage supplies power through a step-up transformer of 0.12 p.u. reactance and a double-circuit line to an infinite bus bar as shown in the figure. The infinite bus voltage is maintained at 1.0 p.u. Neglecting the resistances and susceptances of the system, the steady state stability power limit of the system is 6.25 p.u. If one of the double-circuit is tripped, the resulting steady state stability power limit in p.u. will be

A 50 Hz, 4-pole, 500 MVA, 22 kV turbo-generator is delivering rated megavolt-amperes at 0.8 power factor. Suddenly a fault occurs reducing is electric power output by 40%. Neglect losses and assume constant power input to the shaft. The accelerating torque in the generator in MNm at the time of fault will be