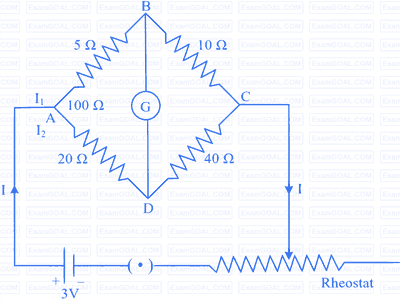
In a given meter bridge, the current flowing through $$40 \Omega$$ resistor is
A potentiometer wire of length $$4 \mathrm{~m}$$ and resistance $$5 ~\Omega$$ is connected in series with a resistance of $$992 ~\Omega$$ and a cell of e.m.f. $$4 \mathrm{~V}$$ with internal resistance $$3 ~\Omega$$. The length of $$0.75 \mathrm{~m}$$ on potentiometer wire balances the e.m.f. of
Two resistance $$\mathrm{X}$$ and $$\mathrm{Y}$$ are connected in the two gaps of a meterbridge and the null points is obtained at $$20 \mathrm{~cm}$$ from zero end. When the resistance of $$20 \Omega$$ is connected in series with the smaller of the two resistance $$\mathrm{X}$$ and $$\mathrm{Y}$$, the null point shifts to $$40 \mathrm{~cm}$$ from left end. The value of smaller resistance in ohm is
Resistance of a potentiometer wire is $$2 \Omega / \mathrm{m}$$. A cell of e.m.f. $$1.5 \mathrm{~V}$$ balances at $$300 \mathrm{~cm}$$. The current through the wire is