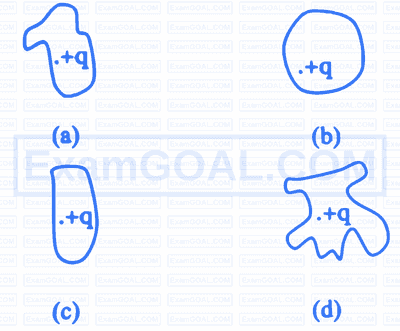
$$ \text { The electric flux through the surface } $$

An electric dipole of length 2 cm is placed with its axis making an angle of $60^{\circ}$ to a uniform electric field of $10^{+5} \mathrm{~N} / \mathrm{C}$. If it experiences a torque of $9 \sqrt{3} \mathrm{Nm}$, the magnitude of the charge on the dipole is $\left(\sin 60^{\circ}=\frac{\sqrt{3}}{2}\right)$

A charge is uniformly distributed on the surface of a spherical rubber balloon. As it is blown up, the total electric flux coming out of the surface

The point charges $+\mathrm{q},-\mathrm{q},-\mathrm{q},+\mathrm{q},+\mathrm{Q}$ and -q are placed at the vertices of a regular hexagon ABCDEF as shown in figure. The electric field at the centre of hexagon ' $O$ ' due to the five charges at $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$ and F is twice the electric field at centre ' O ' due to charge +Q at E alone. The value of $Q$ is