You are asked to evaluate assorted fluid flows for their suitability in a given laboratory application. The following three flow choices. Expressed in terms of the two - dimensional velocity fields in the $$x-$$ $$y$$ plane, are made available.
$$P:$$ $$u = 2y,\,\,\,v = - 3x$$
$$Q:$$ $$u=3xy,$$ $$\,\,\,\,$$$$v=0$$
$$R:$$ $$u=-2x,$$ $$\,\,\,\,$$$$v=2y$$

Which flows should be recommended when the application requires the flow to be incompressible and irrotational?

The gap between a moving circular plate and a stationary surface is being continuously reduced, as the circular plate comes down at a uniform speed $$V$$ towards the stationary bottom surface, as shown in the figure. In the process, the fluid contained between the two plates flows out radially. The fluid is assumed to be incompressible and inviscid.

The radial velocity $${V_r},$$ at any radius $$r$$, when the gap width is $$h,$$ is

The gap between a moving circular plate and a stationary surface is being continuously reduced, as the circular plate comes down at a uniform speed $$V$$ towards the stationary bottom surface, as shown in the figure. In the process, the fluid contained between the two plates flows out radially. The fluid is assumed to be incompressible and inviscid.

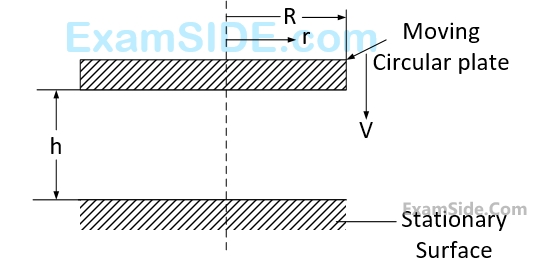
The radial component of the fluid acceleration at $$r=R$$ is

Which combination of the following statements about steady incompressible forced vortex flow is correct?

P: Shear stress is zero at all points in the flow.
Q: Velocity is directly proportional to the radius from the centre of the vortex.
R: Total mechanical energy per unit mass is constant in the entire flow field.
S: Total mechanical energy per unit mass is constant in the entire flow field.