For a steady flow, the velocity field is $$\overrightarrow V = \left( { - {x^2} + 3y} \right)\widehat i + \left( {2xy} \right)\widehat j.$$ The magnitude of the acceleration of the particle at $$(1, -1)$$ is

For a two-dimensional flow, the velocity field is $$\overrightarrow u = {x \over {{x^2} + {y^2}}}\widehat i + {y \over {{x^2} + {y^2}}}\widehat j,$$ where $$\widehat i$$ and $$\widehat j\,\,$$ are the basis vectors in the $$x$$-$$y$$ Cartesian coordinate system .
Identify the CORRECT statements from below.
(1) The flow is incompressible
(2) The flow is unsteady
(3) $$y$$-component of acceleration, $${a_y} = {{ - y} \over {{{\left( {{x^2} + {y^2}} \right)}^2}}}$$
(4) $$x$$-component of acceleration , $${a_x} = {{ - \left( {x + y} \right)} \over {{{\left( {{x^2} + {y^2}} \right)}^2}}}$$

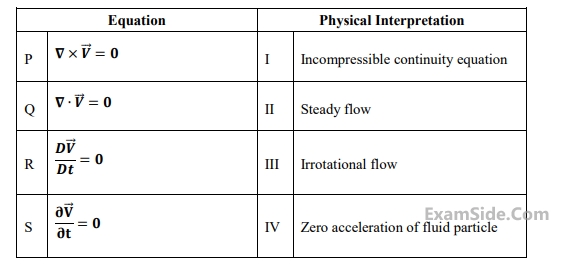
Match the following pairs:

The velocity field on an incompressible flow is given by
$$V = \left( {{a_1}x + {a_2}y + {a_3}z} \right)i + \left( {{b_1}x + {b_2}y + {b_3}z} \right)j$$ $$$ + \left( {{c_1}x + {c_2}y + {c_3}z} \right)k,$$$

Where $${a_1} = 2$$ and $${c_3} = - 4.$$ The value of $${b_2}$$ is _____________.