1
GATE ME 2017 Set 1
MCQ (Single Correct Answer)
+2
-0.6
Two disks A and B with identical mass (m) and radius (R) are initially at rest. They roll down from the top of identical inclined planes without slipping. Disk A has all of its mass concentrated at the rim, while Disk B has its mass uniformly distributed. At the bottom of the plane, the ratio of velocity of the center of disk A to the velocity of the center of disk B is.
2
GATE ME 2016 Set 1
Numerical
+2
-0
A block of mass m rests on an inclined plane and is attached by a string to the wall as shown in the figure. The coefficient of static friction between the plane and the block is $$0.25.$$ The string can withstand a maximum force of $$20$$ N. The maximum value of the mass (m) for which the string will not break and the block will be in static equilibrium is ____________ kg.
Take $$\cos \theta = 0.8$$ and $$\sin \theta = 0.6$$. Acceleration due to gravity g $$=$$ $$10$$ m/s2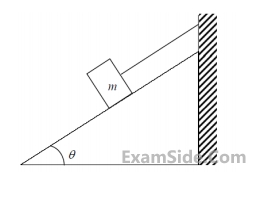
Take $$\cos \theta = 0.8$$ and $$\sin \theta = 0.6$$. Acceleration due to gravity g $$=$$ $$10$$ m/s2

Your input ____
3
GATE ME 2016 Set 1
MCQ (Single Correct Answer)
+2
-0.6
A two-member truss $$PQR$$ is supporting a load W. The axial forces in members $$PQ$$ and $$QR$$ are respectively
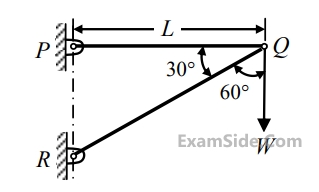

4
GATE ME 2016 Set 3
Numerical
+2
-0
A circular disc of radius 100 mm and mass 1 kg, initially at rest at position A, rolls without slipping down a curved path as shown in figure. The speed v of the disc when it reaches position B is _________ m/s.
Acceleration due to gravity g = 10 m/s2
Acceleration due to gravity g = 10 m/s2

Your input ____
Questions Asked from Engineering Mechanics Static and Dynamics (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ME 2024 (1)
GATE ME 2023 (1)
GATE ME 2022 Set 2 (4)
GATE ME 2022 Set 1 (3)
GATE ME 2017 Set 2 (1)
GATE ME 2017 Set 1 (1)
GATE ME 2016 Set 1 (2)
GATE ME 2016 Set 3 (3)
GATE ME 2016 Set 2 (1)
GATE ME 2015 Set 2 (2)
GATE ME 2015 Set 1 (2)
GATE ME 2015 Set 3 (1)
GATE ME 2014 Set 1 (3)
GATE ME 2014 Set 4 (4)
GATE ME 2014 Set 2 (1)
GATE ME 2014 Set 3 (3)
GATE ME 2013 (1)
GATE ME 2012 (2)
GATE ME 2011 (1)
GATE ME 2009 (1)
GATE ME 2008 (2)
GATE ME 2007 (1)
GATE ME 2006 (1)
GATE ME 2005 (4)
GATE ME 2004 (3)
GATE ME 2003 (2)
GATE ME 1999 (1)
GATE ME 1997 (1)
GATE ME 1996 (3)
GATE ME 1995 (1)
GATE ME Subjects
Engineering Mechanics
Machine Design
Strength of Materials
Heat Transfer
Production Engineering
Industrial Engineering
Turbo Machinery
Theory of Machines
Engineering Mathematics
Fluid Mechanics
Thermodynamics
General Aptitude