A three-hinge arch ABC in the form of a semi-circle is shown in the figure. The arch is in static equilibrium under vertical loads of $P = 100$ kN and $Q = 50$ kN. Neglect friction at all the hinges. The magnitude of the horizontal reaction at B is _________ kN (rounded off to 1 decimal place).

A spherical ball weighing 2 kg is dropped from a height of 4.9 m onto an immovable rigid block as shown in the figure. If the collision is perfectly elastic, what is the momentum vector of the ball (in kg m/s) just after impact?
Take the acceleration due to gravity to be 𝑔 = 9.8 m/s2. Options have been rounded off to one decimal place.

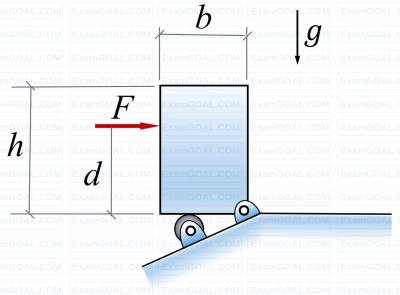
A rigid homogeneous uniform block of mass 1 kg, height h = 0.4 m and width b = 0.3 m is pinned at one corner and placed upright in a uniform gravitational field (g = 9.81 m/s2), supported by a roller in the configuration shown in the figure. A short duration (impulsive) force F, producing an impulse IF is applied at a height of d = 0.3 m from the bottom as shown. Assume all joints to be frictionless. The minimum value of IF required to topple the block is
A rigid body in the X-Y plane consists of two point masses (1 kg each) attached to the ends of two massless rods, each of 1 cm length, as shown in the figure. It rotates at 30 RPM counter-clockwise about the Z-axis passing through point O. A point mass of √2 kg, attached to one end of a third massless rod, is used for balancing the body by attaching the free end of the rod to point O. The length of the third rod is ______ cm.
