GATE ME 2014 Set 3 | Simple Stress and Strain Question 21 | Strength of Materials

GATE ME 2014 Set 3

MCQ (Single Correct Answer)

-0.3

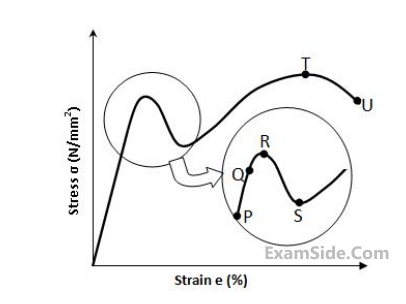
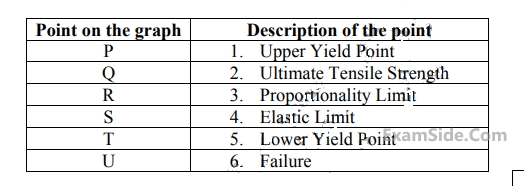
The stress-strain curve for mild steel is shown in the figure given below. Choose the correct option referring to both figure and table GATE ME 2014 Set 3 Strength of Materials - Simple Stress and Strain Question 25 English 1

GATE ME 2014 Set 3 Strength of Materials - Simple Stress and Strain Question 25 English 1

GATE ME 2014 Set 3 Strength of Materials - Simple Stress and Strain Question 25 English 2

$$P - 1,\,Q - 2,\,R - 3,\,S - 4,\,T - 5,\,U - 6$$

$$P - 3,\,Q - 1,\,R - 4,\,S - 2,\,T - 6,\,U - 5$$

$$P - 3,\,Q - 4,\,R - 1,\,S - 5,\,T - 2,\,U - 6$$

$$P - 4,\,Q - 1,\,R - 5,\,S - 2,\,T - 3,\,U - 6$$

GATE ME 2013

MCQ (Single Correct Answer)

-0.3

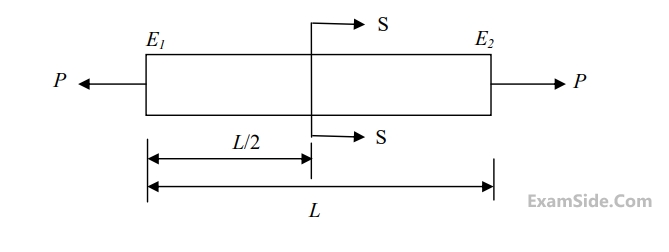
A rod of length $$L$$ having uniform cross-sectional area $$A$$ is subjected to a tensile force $$P$$ as shown in the figure below. If the Young’s modulus of the material varies linearly from $${E_1}$$ to $${E_2}$$ along the length of the rod, the normal stress developed at the section $$-$$ $$SS$$ is GATE ME 2013 Strength of Materials - Simple Stress and Strain Question 30 English

GATE ME 2013 Strength of Materials - Simple Stress and Strain Question 30 English

$${P \over A}$$

$${{P\left( {{E_1} - {E_2}} \right)} \over {A\left( {{E_1} + {E_2}} \right)}}$$

$${{P{E_2}} \over {A{E_1}}}$$

$${{P{E_1}} \over {A{E_2}}}$$

GATE ME 2007

MCQ (Single Correct Answer)

-0.3

A steel rod of length $$L$$ and diameter $$D$$, fixed at both ends, is uniformly heated to a temperature rise of $$\Delta T.$$ The Young's modulus is $$E$$ and the coefficient of linear expansion is $$'\alpha '\,.$$ The thermal stress in the rod is

$$0$$

$$\alpha \Delta \,T$$

$$E\alpha \Delta \,T$$

$$E\alpha \Delta \,TL$$

GATE ME 2004

MCQ (Single Correct Answer)

-0.3

A uniform, slender cylindrical rod is made of a homogeneous and isotropic material. The rod rests on a frictionless surface. The rod is heated uniformly. If the radial and longitudinal thermal stresses are represented by $${\sigma _r}$$ and $${\sigma _z}$$ respectively, then

$${\sigma _r} = 0,{\sigma _z} = 0$$

$${\sigma _r} \ne 0,{\sigma _z} = 0$$

$${\sigma _r} = 0,{\sigma _z} \ne 0$$

$${\sigma _r} \ne 0,{\sigma _z} \ne 0$$

PREVIOUS NEXT