1
GATE ME 2022 Set 1
Numerical
+1
-0
A rigid uniform annular disc is pivoted on a knife edge A in a uniform gravitational field as shown, such that it can execute small amplitude simple harmonic motion in the plane of the figure without slip at the pivot point. The inner radius r and outer radius 𝑅 are such that r2 = R2/2, and the acceleration due to gravity is g. If the time period of small amplitude simple harmonic motion is given by $T = β π \sqrt{R/g} $ where π is the ratio of circumference to diameter of a circle, then β = ________ (round off to 2 decimal places).
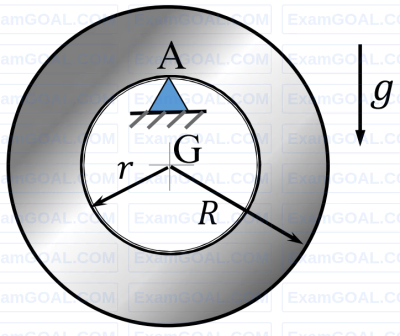
Your input ____
2
GATE ME 2017 Set 2
MCQ (Single Correct Answer)
+1
-0.3
A mass $$m$$ is attached to two identical springs having spring constant $$k$$ as shown in the figure. The natural frequency of this single degree of freedom system is
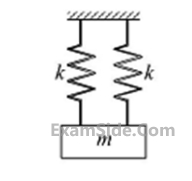

3
GATE ME 2017 Set 1
MCQ (Single Correct Answer)
+1
-0.3
The damping ratio for a viscously damped spring mass system, governed by the relationship $$\,m{{{d^2}x} \over {d{t^2}}} + c{{dx} \over {dt}} + kx = f\left( t \right),\,\,\,$$ is given by
4
GATE ME 2016 Set 3
Numerical
+1
-0
The static deflection of a spring under gravity, when a mass of 1 kg is suspended from it, is 1 mm. Assume the acceleration due to gravity g =10 m/s2 . The natural frequency of this spring-mass system (in rad/s) is _____________
Your input ____
Questions Asked from Vibrations (Marks 1)
Number in Brackets after Paper Indicates No. of Questions
GATE ME 2025 (2)
GATE ME 2024 (1)
GATE ME 2023 (1)
GATE ME 2022 Set 2 (1)
GATE ME 2022 Set 1 (1)
GATE ME 2017 Set 2 (1)
GATE ME 2017 Set 1 (1)
GATE ME 2016 Set 3 (1)
GATE ME 2016 Set 1 (1)
GATE ME 2015 Set 2 (1)
GATE ME 2015 Set 3 (1)
GATE ME 2014 Set 4 (1)
GATE ME 2014 Set 3 (1)
GATE ME 2014 (2)
GATE ME 2013 (1)
GATE ME 2010 (1)
GATE ME 2009 (1)
GATE ME 2007 (1)
GATE ME 2006 (1)
GATE ME 2005 (1)
GATE ME 2004 (1)
GATE ME 2001 (1)
GATE ME Subjects
Engineering Mechanics
Strength of Materials
Theory of Machines
Engineering Mathematics
Machine Design
Fluid Mechanics
Turbo Machinery
Heat Transfer
Thermodynamics
Production Engineering
Industrial Engineering
General Aptitude