For a dynamical system governed by the equation,

$\ddot{x}(t)+2 ζ \omega_n \dot{x}(t)+\omega_n^2x(t)=0$

the damping ratio ζ is equal to $\frac{1}{2\pi}\log_e2$. The displacement x of this system is measured during a hammer test. A displacement peak in the positive displacement direction is measured to be 4 mm. Neglecting higher powers (> 1) of the damping ratio, the displacement at the next peak in the positive direction will be _______ mm (in integer).

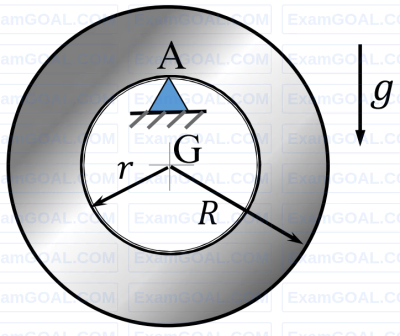
A rigid uniform annular disc is pivoted on a knife edge A in a uniform gravitational field as shown, such that it can execute small amplitude simple harmonic motion in the plane of the figure without slip at the pivot point. The inner radius r and outer radius 𝑅 are such that r² = R²/2, and the acceleration due to gravity is g. If the time period of small amplitude simple harmonic motion is given by $T = β π \sqrt{R/g} $ where π is the ratio of circumference to diameter of a circle, then β = ________ (round off to 2 decimal places).

A mass $$m$$ is attached to two identical springs having spring constant $$k$$ as shown in the figure. The natural frequency of this single degree of freedom system is

The damping ratio for a viscously damped spring mass system, governed by the relationship $$\,m{{{d^2}x} \over {d{t^2}}} + c{{dx} \over {dt}} + kx = f\left( t \right),\,\,\,$$ is given by