GATE ME 2006 | Conduction Question 23 | Heat Transfer

GATE ME 2006

MCQ (Single Correct Answer)

-0.3

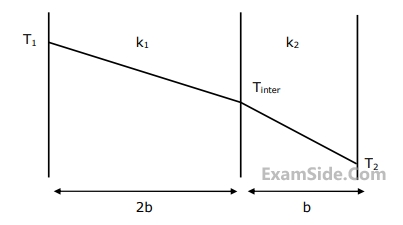
In a composite slab, the temperature at the interface (T_inter) between two materials is equal to the average of the temperatures at the two ends. Assuming steady one-dimensional heat conduction, which of the following statements is true about the respective thermal conductivities? GATE ME 2006 Heat Transfer - Conduction Question 37 English

GATE ME 2006 Heat Transfer - Conduction Question 37 English

$$2{K_1} = {K_2}$$

$${K_1} = {K_2}$$

$$2{K_1} = 3{K_2}$$

$${K_1} = 2{K_2}$$v

GATE ME 2005

MCQ (Single Correct Answer)

-0.3

In case of one dimensional heat conduction in a medium with constant properties, $$T$$ is the temperature at position $$x,$$ at time $$t.$$ Then $${{\partial T} \over {\partial t}}$$ is proportional to

$${T \over x}$$

$${{\partial T} \over {\partial x}}$$

$${{{\partial ^2}T} \over {\partial x\partial t}}$$

$${{{\partial ^2}T} \over {\partial {x^2}}}$$

GATE ME 2004

MCQ (Single Correct Answer)

-0.3

One dimensional unsteady state heat transfer equation for a sphere with heat generation at the rate $$'{q_g}',$$ can be written as

$${1 \over {r^2}}\,{\partial \over {\partial r}}\left( {r{{\partial T} \over {\partial r}}} \right) + {q \over k} = {1 \over \alpha }\,{{\partial T} \over {\partial t}}$$

$${1 \over {r^2}}\,{\partial \over {\partial r}}\left( {{r^2}{{\partial T} \over {\partial r}}} \right) + {q \over k} = {1 \over \alpha }\,{{\partial T} \over {\partial t}}$$

$${{{\partial ^2}T} \over {\partial {r^2}}} + {q \over k} = {1 \over \alpha }\,{{\partial T} \over {\partial t}}$$

$${{{\partial ^2}} \over {\partial {r^2}}}\left( {rT} \right) + {q \over k} = {1 \over \alpha }\,{{\partial T} \over {\partial t}}$$

GATE ME 2001

MCQ (Single Correct Answer)

-0.3

In descending order of magnitude, the thermal conductivity of $$(a)$$ Pure iron, $$(b)$$ liquid water, $$(c)$$ saturated water vapour, and $$(d)$$ aluminum can be arranged as

$$a\,\,b\,\,c\,\,d$$

$$b\,\,c\,\,a\,\,d$$

$$d\,\,a\,\,b\,\,c$$

$$d\,\,c\,\,b\,\,a$$

PREVIOUS NEXT