A steady laminar boundary layer is formed over a flat plate as shown in the figure. The free stream velocity of the fluid is $${U_0}.$$ The velocity profile at the inlet $$a$$-$$b$$ is uniform, while that at a downstream location $$c$$-$$d$$ is
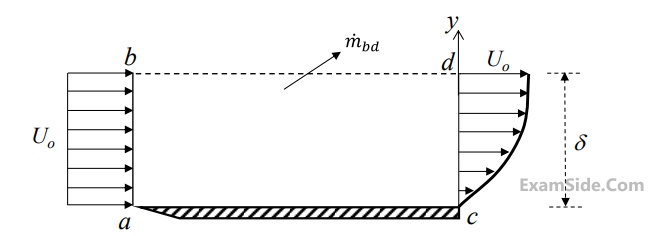
given by $$u = {U_0}\left[ {2\left( {{y \over \delta }} \right) - {{\left( {{y \over \delta }} \right)}^2}} \right]$$

The ratio of the mass flow rate, $$\mathop {m{}_{bd}}\limits^ \bullet ,$$ leaving through the horizontal section $$b$$-$$d$$ to that entering through the vertical section $$a$$-$$b$$ is

Air ( $${\rho = 1.2\,\,kg/{m^3}}$$ and kinematic viscosity, $${v = 2 \times {{10}^{ - 5}}{m^2}/s}$$ ) with a velocity of $$2m/s$$ flows over the top surface of a flat plate of length $$2.5m.$$ If the average value of friction coefficient is $${C_f} = {{1.328} \over {\sqrt {{{{\mathop{\rm Re}\nolimits} }_x}} }},\,\,$$ the total drag force (in $$N$$) per unit width of the plate is ____________

An incompressible fluid flows over a flat plate with zero pressure gradient. The boundary layer thickness is $$1mm$$ at a location where the Reynolds number is $$1000$$. If the velocity of the fluid alone is increased by a factor of $$4,$$ then the boundary layer thickness sat the same location, in $$mm$$ will be

Consider a steady incompressible flow through a channel as shown below.

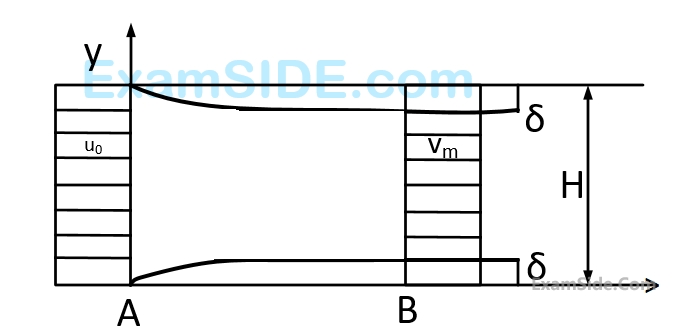
The velocity profile is uniform with a value of $${u_0}$$ at the inlet section $$A$$. The velocity profile at section B down stream is

$$$u\left\{ {\matrix{ {{V_m}{y \over \delta },} & {0 \le y \le \delta } \cr {{V_m},} & {\delta \le y \le H - \delta } \cr {{V_m}{{H - y} \over \delta },} & {H - \delta \le y \le H} \cr } } \right.$$$

The ratio $${{{P_A} - {P_B}} \over {{1 \over 2}\rho {u_0}^2}}$$ (where $${{P_A}}$$ and $${{P_B}}$$ are the pressure at section $$A$$ and $$B$$ respectively and $$\rho $$ is the density of the fluid ) is