Consider a steady incompressible flow through a channel as shown below.

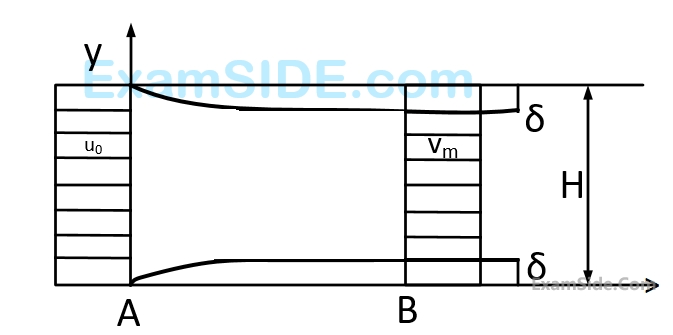
The velocity profile is uniform with a value of $${u_0}$$ at the inlet section $$A$$. The velocity profile at section B down stream is

$$$u\left\{ {\matrix{ {{V_m}{y \over \delta },} & {0 \le y \le \delta } \cr {{V_m},} & {\delta \le y \le H - \delta } \cr {{V_m}{{H - y} \over \delta },} & {H - \delta \le y \le H} \cr } } \right.$$$

The ratio $${{{V_m}} \over {{u_0}}}$$ is

A smooth flat plate with a sharp leading edge is placed along a gas stream flowing at $$U = 10\,m/s.$$ The thickness of the boundary layer at section $$r$$- $$s$$ is $$10$$ $$mm,$$ the breadth of the plate is $$1$$ $$m$$ (into the paper) and the density of the gas, $$\rho = 1.0\,kg/{m^3}.$$ Assume that the boundary layer is thin, two-dimensional, and follows a linear velocity distribution, $$u = U\left( {y/\delta } \right),$$ at the section $$r$$-$$s$$, where $$y$$ is the height from plate.

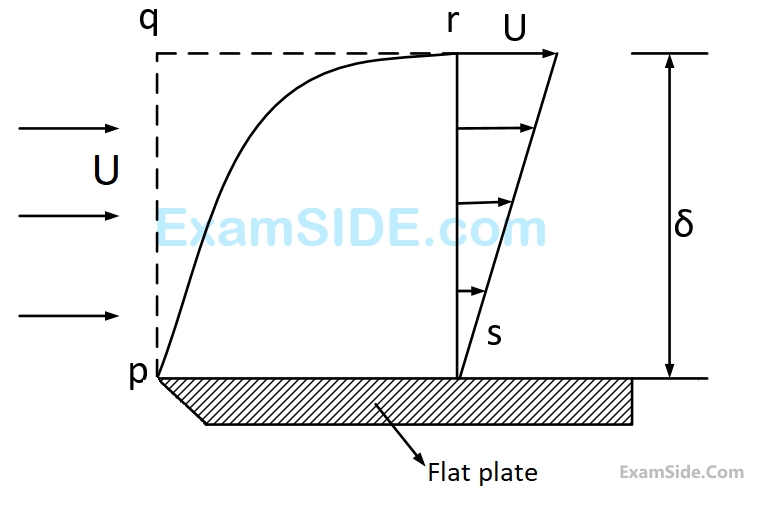
The mass flow rate (in kg/s) across the section $$q$$-$$r$$ is

A smooth flat plate with a sharp leading edge is placed along a gas stream flowing at $$U = 10\,m/s.$$ The thickness of the boundary layer at section $$r$$- $$s$$ is $$10$$ $$mm,$$ the breadth of the plate is $$1$$ $$m$$ (into the paper) and the density of the gas, $$\rho = 1.0\,kg/{m^3}.$$ Assume that the boundary layer is thin, two-dimensional, and follows a linear velocity distribution, $$u = U\left( {y/\delta } \right),$$ at the section $$r$$-$$s$$, where $$y$$ is the height from plate.

The integrated drag force (in $$N$$) on the plate, between $$p$$-$$s$$, is

For air flow over a flat plate, velocity $$(U)$$ and boundary layer thickness $$\left( \delta \right)$$ can be expressed respectively, as $$${U \over {{U_\infty }}} = {3 \over 2}{y \over \delta } - {1 \over 2}{\left( {{y \over \delta }} \right)^3}\,\,\,\,;\,\,\,\,\delta = {{4.64x} \over {\sqrt {{{{\mathop{\rm Re}\nolimits} }_x}} }}$$$
If the free stream velocity is $$2$$ $$m/s$$, and air has Kinematic viscosity of $$1.5 \times {10^{ - 5}}{m^2}/s$$ and density of $$1.23$$ $$kg/{m^3}$$, then wall shear stress at $$x=1$$ $$m$$, is