A cascade system having the impulse responses $$$\begin{array}{l}h_1\left(n\right)=\left\{1,\;-1\right\}\;\;\;and\;\;h_2\left(n\right)=\left\{1,\;1\right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$$ is shown in the figure below, where symbol $$\uparrow$$ denotes the time origin. 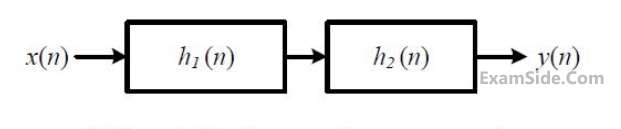The input sequence x(n) for which the cascade system produces an output sequence $$$\begin{array}{l}y\left(n\right)=\left\{1,\;2,\;1,\;-1,\;-2,\;-1\right\}\;\;is\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$$

Consider a discrete time signal given by
x[n]=(-0.25)ⁿu[n]+(0.5)ⁿu[-n-1]
The region of convergence of its Z-transform would be

A discrete system is represented by the difference equation $$$\begin{bmatrix}X_1\left(k+1\right)\\X_2\left(k+2\right)\end{bmatrix}=\begin{bmatrix}a&a-1\\a+1&a\end{bmatrix}\begin{bmatrix}X_1\left(k\right)\\X_2\left(k\right)\end{bmatrix}$$$ It has initial condition $$X_1\left(0\right)=1;\;X_2\left(0\right)=0$$. The pole location of the system for a = 1, are

Let $$X\left(z\right)=\frac1{1-z^{-3}}$$ be the Z–transform of a causal signal x[n]. Then, the values of x[2] and x[3] are