Two identical long parallel wires carry currents ' $\mathrm{I}_1$ ' and ' $\mathrm{I}_2$ ' such that $\mathrm{I}_1>\mathrm{I}_2$. When the currents are in the same direction, the magnetic field at a point midway between the wires is $8 \times 10^{-6} \mathrm{~T}$. If the direction of $\mathrm{I}_2$ is reversed, the field becomes $3.2 \times 10^{-5} \mathrm{~T}$. The ratio of $\mathrm{I}_2$ to $\mathrm{I}_1$ is

An element $\overrightarrow{\Delta l}=\Delta \mathrm{xi}$ is placed at the origin and carries a current of 10 A . The magnitude of magnetic field on the Y axis at a distance of 0.5 m if $\Delta x=1 \mathrm{~cm}$ is $\left(\frac{\mu_0}{4 \pi}=10^{-7}\right.$ SI unit $)\left(\sin 90^{\circ}=1\right)$

A current ' I ' is flowing in a conductor PQRST as shown in figure. The radius of curved path QRS is ' R ' and length of straight portion PQ and ST is very large. The magnetic field at the centre $[\mathrm{O}]$ of the curved part is ( $\mu_0=$ permeability of free space)

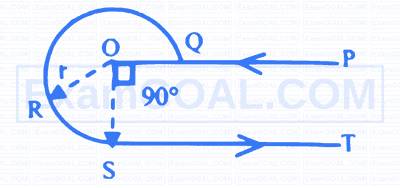
A wire has three different sections as shown in figure. The magnitude of the magnetic field produced at the centre ' $O$ ' of the semicircle by three sections together is ( $\mu_0=$ permiability of free space)