Water enters a tube of diameter, $D=60 \mathrm{~mm}$ with mass flow rate of $0.01 \mathrm{~kg} \mathrm{~s}^{-1}$ as shown in the figure below. The inlet mean temperature is $T_{m, i}=293 \mathrm{~K}$ and the uniform heat flux at the surface of the tube is $2000 \mathrm{Wm}^{-2}$. For the exit mean temperature of $T_{m, o}=$ 353 K , the length of the tube, $L$ is ___________ m (rounded off to 1 decimal place). Use the specific heat of water as $4181 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}$.

Consider a slab of 20 mm thickness. There is a uniform heat generation of $ \dot{q} = 100 \text{ MW/m}^3 $ inside the slab. The left and right faces of the slab are maintained at 150 °C and 110 °C, respectively. The plate has a constant thermal conductivity of 200 W/(m.K). Considering a 1-D steady state heat conduction, the location of the maximum temperature from the left face will be at ______mm (answer in integer).

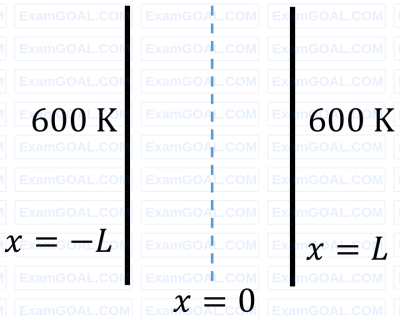
Consider steady state, one-dimensional heat conduction in an infinite slab of thickness 2L (L = 1 m) as shown in the figure. The conductivity (k) of the material varies with temperature as k = CT, where T is the temperature in K, and C is a constant equal to 2 W.m-1K-2. There is a uniform heat generation of 1280 kW/m3 in the slab. If both faces of the slab are maintained at 600 K, then the temperature at x = 0 is _______ K (in integer).
Consider a rod of uniform thermal conductivity whose one end (x = 0) is insulated and the other end (x = L) is exposed to flow of air at temperature T∞ with convective heat transfer coefficient h. The cylindrical surface of the rod is insulated so that the heat transfer is strictly along the axis of the rod. The rate of internal heat generation per unit volume inside the rod is given as
$\rm \dot q = \cos \frac{2 \pi x}{L}$
The steady-state temperature at the mid-location of the rod is given as TA. What will be the temperature at the same location, if the convective heat transfer coefficient increases to 2h?