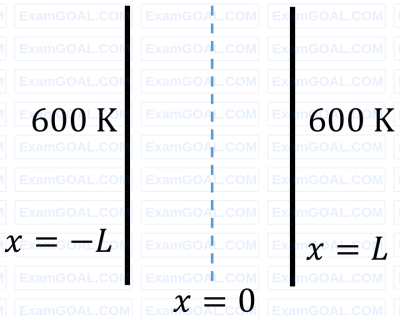
Consider steady state, one-dimensional heat conduction in an infinite slab of thickness 2L (L = 1 m) as shown in the figure. The conductivity (k) of the material varies with temperature as k = CT, where T is the temperature in K, and C is a constant equal to 2 W.m-1K-2. There is a uniform heat generation of 1280 kW/m3 in the slab. If both faces of the slab are maintained at 600 K, then the temperature at x = 0 is _______ K (in integer).
Consider a rod of uniform thermal conductivity whose one end (x = 0) is insulated and the other end (x = L) is exposed to flow of air at temperature T∞ with convective heat transfer coefficient h. The cylindrical surface of the rod is insulated so that the heat transfer is strictly along the axis of the rod. The rate of internal heat generation per unit volume inside the rod is given as
$\rm \dot q = \cos \frac{2 \pi x}{L}$
The steady-state temperature at the mid-location of the rod is given as TA. What will be the temperature at the same location, if the convective heat transfer coefficient increases to 2h?
Consider a solid slab (thermal conductivity, k = 10 W∙m-1∙K-1) with thickness 0.2 m and of infinite extent in the other two directions as shown in the figure. Surface 2, at 300 K, is exposed to a fluid flow at a free stream temperature (T∞) of 293 K, with a convective heat transfer coefficient (h) of 100 W∙m-2∙K-1. Surface 2 is opaque, diffuse and gray with an emissivity (ε) of 0.5 and exchanges heat by radiation with very large surroundings at 0 K. Radiative heat transfer inside the solid slab is neglected. The Stefan-Boltzmann constant is 5.67 × 10-8 W∙m-2∙K-4. The temperature T1 of Surface 1 of the slab, under steady-state conditions, is _________ K (round off to the nearest integer).
