Consider a steady flow through a horizontal divergent channel, as shown in the figure, with the supersonic flow at the inlet. The direction of flow is from left to right.
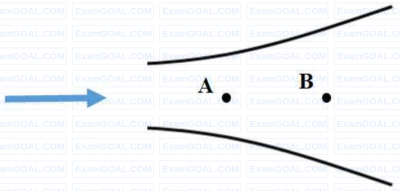
Pressure at location B is observed to be higher than that at an upstream location A. Which among the following options can be the reason?
In the following two-dimensional momentum equation for natural convection over a surface immersed in a quiescent fluid at temperature T∞ (g is the gravitational acceleration, β is the volumetric thermal expansion coefficient, ν is the kinematic viscosity, u and v are the velocities in x and y directions, respectively, and T is the temperature)
$\rm u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = g β (T - T_∞) + \nu \frac{\partial^2 u}{\partial y^2} $
the term gβ(T - T∞) represent
The figure shows a purely convergent nozzle with a steady, inviscid compressible flow of an ideal gas with constant thermophysical properties operating under choked condition. The exit plane shown in the figure is located within the nozzle. If the inlet pressure (P0) is increased while keeping the back pressure (Pback) unchanged, which of the following statements is/are true?
