In a laboratory experiment using a scaled down model to measure scour at a bridge pier, the Froude number is important. The ratio of the prototype length to the model length is 100 . If the velocity of the model is $1 \mathrm{~m} \mathrm{~s}^{-1}$, the velocity (in $\mathrm{m} \mathrm{s}^{-1}$ ) of the prototype is

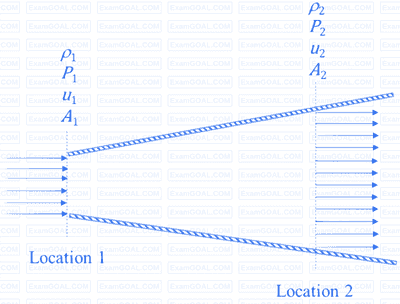
Consider an isentropic flow of air (ratio of specific heats = 1.4) through a duct as shown in the figure.

The variations in the flow across the cross-section are negligible. The flow conditions at Location 1 are given as follows:

𝑃₁ = 100 kPa, 𝜌₁ = 1.2 kg/m³ , 𝑢₁= 400 m/s

The duct cross-sectional area at Location 2 is given by A₂ = 2A₁, where A₁ denotes the duct cross-sectional area at Location 1. Which one of the given statements about the velocity 𝑢₂ and pressure 𝑃₂ at Location 2 is TRUE? 

Consider a steady flow through a horizontal divergent channel, as shown in the figure, with the supersonic flow at the inlet. The direction of flow is from left to right.

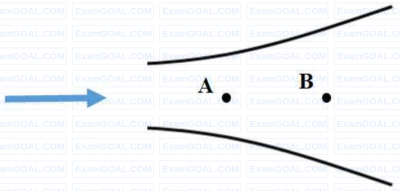
Pressure at location B is observed to be higher than that at an upstream location A. Which among the following options can be the reason?

In the following two-dimensional momentum equation for natural convection over a surface immersed in a quiescent fluid at temperature T_∞ (g is the gravitational acceleration, β is the volumetric thermal expansion coefficient, ν is the kinematic viscosity, u and v are the velocities in x and y directions, respectively, and T is the temperature)

$\rm u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = g β (T - T_∞) + \nu \frac{\partial^2 u}{\partial y^2} $

the term gβ(T - T_∞) represent