GATE EE 2010 | Linear Time Invariant Systems Question 25 | Signals and Systems

GATE EE 2010

MCQ (Single Correct Answer)

-0.6

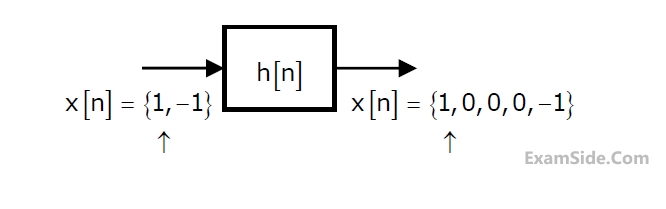
Given the finite length input x[n] and the corresponding finite length output y[n] of an LTI system as shown below, the impulse response h[n] of the system is GATE EE 2010 Signals and Systems - Linear Time Invariant Systems Question 37 English

GATE EE 2010 Signals and Systems - Linear Time Invariant Systems Question 37 English

$$\begin{array}{l}h\left[n\right]=\left\{1,\;0,\;0,\;1\right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$

$$\begin{array}{l}h\left[n\right]=\left\{1,\;0,\;1\right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$

$$\begin{array}{l}h\left[n\right]=\left\{1,\;1,\;1,\;1\right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$

$$\begin{array}{l}h\left[n\right]=\left\{1,\;1,\;1\right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$

GATE EE 2009

MCQ (Single Correct Answer)

-0.6

A cascade of 3 Linear Time Invariant systems is casual and unstable. From this, we conclude that

each system in the cascade is individually casual and unstable

at least one system is unstable and atleast one system is casual

at least one system is casual and all systems are unstable

the majority are unstable and the majority are casual

GATE EE 2009

MCQ (Single Correct Answer)

-0.6

The $$z$$$$-$$ transform of a signal $$x\left[ n \right]$$ is given by $$4{z^{ - 3}} + 3{z^{ - 1}} + 2 - 6{z^2} + 2{z^3}.$$ It is applied to a system, with a transfer function $$H\left( z \right) = 3{z^{ - 1}} - 2.$$ Let the output be $$y(n)$$. Which of the following is true?

$$y\left( n \right)$$ is non causal with finite support

$$y\left( n \right)$$ is causal with infinite support

$$y\left( n \right)$$ $$ = 0;\,|n| > 3$$

$$\eqalign{ & {\mathop{\rm Re}\nolimits} {\left[ {Y\left( z \right)} \right]_{z = {e^{j0}}}} = - {\mathop{\rm Re}\nolimits} {\left[ {Y\left( z \right)} \right]_{z = {e^{j0}}}}; \cr & {\rm I}m{\left[ {Y\left( z \right)} \right]_{z = {e^{j0}}}}\, = {\rm I}m{\left[ {Y\left( z \right)} \right]_z} = {e^{j0}};\,\, - \pi \le \theta < \pi \cr} $$

GATE EE 2008

MCQ (Single Correct Answer)

-0.6

A system with input $$x(t)$$ and output $$y(t)$$ is defined by the input $$-$$ output relation:
$$y\left( t \right) = \int\limits_{ - \infty }^{ - 2t} {x\left( \tau \right)} d\tau .$$ The system will be

causal, time $$-$$ invariant and unstable

causal, time $$-$$ invariant and stable

non $$-$$ causal, time $$-$$ invariant and unstable

non $$-$$ causal, time $$-$$ variant and unstable

PREVIOUS NEXT