A synchronous generator is to be connected to an infinite bus through a transmission line of reactance X = 0.2 pu, as shown in figure the generator data is as follows:

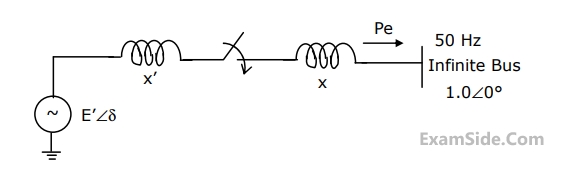
X¹ = 0.1 pu, E¹ = 1.0 pu, H = 5 MJ/MVA, mechanical power P_m = 0.0 pu, $$\omega $$_B = 2 $$\pi \times $$50 rad/sec. All quantities are expressed on a common base.

The generator is initially running on open circuit with the frequency of the open circuit voltage slightly higher than that of the infinite bus. If at the instant of switch closure $$\delta = 0$$ and $$\omega = {{d\delta } \over {dt}} = {\omega _{init}},$$ compute the maximum value of $${\omega _{init}}$$ so that the generator pulls into synchronism.

$$\int {\left( {{{2H} \over {{\omega _B}}}} \right)\omega d\omega + {P_e}d\delta = 0} $$

A synchronous generator is connected to an infinite bus through a lossless double circuit transmission line. The generator is delivering 1.0 per unit power at a load angle of $${30^0}$$ when a sudden fault reduces the peak power that can be transmitted to 0.5 per unit. After clearance of fault, the peak power that can be transmitted becomes 1.5 per unit. Find the critical clearing angle.

A synchronous generator, having a reactance of 0.15 p.u., is connected to an infinite bus through two identical parallel transmission lines having reactance of 0.3 p.u. each. In steady state, the generator is delivering 1 p.u. Power to the infinite bus. For a three phase fault at the receiving end of one line, calculate the rotor angle at the end of first time step of 0.05 seconds. Assume the voltage behind transient reactance for the generator as 1.1 p.u. and infinite bus voltage as 1.0 p.u. Also indicate how the accelerating powers will be evaluated for the next time step if the breaker clears the fault.

(i) at the end of an interval
(ii) at the middle of an interval.

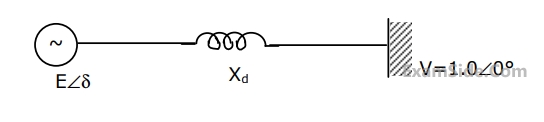
An alternator is connected to an infinite bus as shown in figure. It delivers 1.0 p.u. current at 0.8 p.f lagging at V = 1.0 p.u.. The reactance X_d of the alternator is 1.2 p.u. Determine the active power output and the steady state power limit. Keeping the active power fixed, if the excitation is reduced, find the critical excitation corresponding to operation at stability limit.