1
GATE ME 2016 Set 1
MCQ (Single Correct Answer)
+2
-0.6
A solid disc with radius a is connected to a spring at a point $$d$$ above the center of the disc. The other end of the spring is fixed to the vertical wall. The disc is free to roll without slipping on the ground. The mass of the disc is $$M$$ and the spring constant is $$K$$. The polar moment of inertia for the disc about its centre is $$J = {{M{a^2}} \over 2}$$
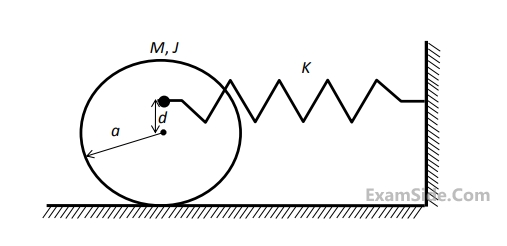

The natural frequency of this system in rad/s is given by
2
GATE ME 2016 Set 3
Numerical
+2
-0
A single degree of freedom spring-mass system is subjected to a harmonic force of constant amplitude. For an excitation frequency of $$\sqrt {{{3k} \over m}} ,$$ the ratio of the amplitude of steady state response to the static deflection of the spring is __________
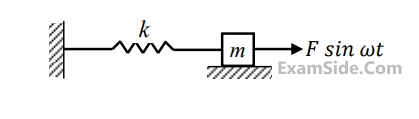

Your input ____
3
GATE ME 2016 Set 2
Numerical
+2
-0
The system shown in the figure consists of block A of mass 5 kg connected to a spring through a massless rope passing over pulley B of radius r and mass 20 kg. The spring constant k is 1500 N/m. If there is no slipping of the rope over the pulley, the natural frequency of the system is_____________ rad/s.
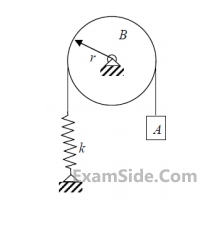

Your input ____
4
GATE ME 2015 Set 2
MCQ (Single Correct Answer)
+2
-0.6
A single-degree-freedom spring mass system is subjected to a sinusoidal force of $$10$$ N amplitude and frequency $$\omega $$ along the axis of the spring. The stiffness of the spring is $$150$$N/m, damping factor is $$0.2$$ and the undamped natural frequency is $$10$$$$\omega $$. At steady state, the amplitude of vibration (in m) is approximately
Questions Asked from Vibrations (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ME 2025 (1)
GATE ME 2024 (1)
GATE ME 2022 Set 2 (1)
GATE ME 2022 Set 1 (1)
GATE ME 2017 Set 2 (1)
GATE ME 2017 Set 1 (1)
GATE ME 2016 Set 1 (1)
GATE ME 2016 Set 3 (1)
GATE ME 2016 Set 2 (1)
GATE ME 2015 Set 2 (1)
GATE ME 2015 Set 1 (3)
GATE ME 2015 Set 3 (1)
GATE ME 2014 Set 1 (2)
GATE ME 2014 Set 4 (1)
GATE ME 2014 Set 2 (1)
GATE ME 2014 Set 3 (2)
GATE ME 2013 (1)
GATE ME 2012 (1)
GATE ME 2011 (2)
GATE ME 2010 (1)
GATE ME 2009 (2)
GATE ME 2008 (2)
GATE ME 2007 (2)
GATE ME 2006 (3)
GATE ME 2005 (1)
GATE ME 2004 (2)
GATE ME 2003 (3)
GATE ME 2001 (1)
GATE ME 2000 (1)
GATE ME 1999 (1)
GATE ME 1996 (1)
GATE ME Subjects
Engineering Mechanics
Strength of Materials
Theory of Machines
Engineering Mathematics
Machine Design
Fluid Mechanics
Turbo Machinery
Heat Transfer
Thermodynamics
Production Engineering
Industrial Engineering
General Aptitude