1
GATE ME 2015 Set 1
MCQ (Single Correct Answer)
+2
-0.6
A mobile phone has a small motor with an eccentric mass used for vibrator mode. The location of the eccentric mass on motor with respect to center of gravity $$(CG)$$ of the mobile and the rest of the dimensions of the mobile phone are shown. The mobile is kept on a flat horizontal surface.
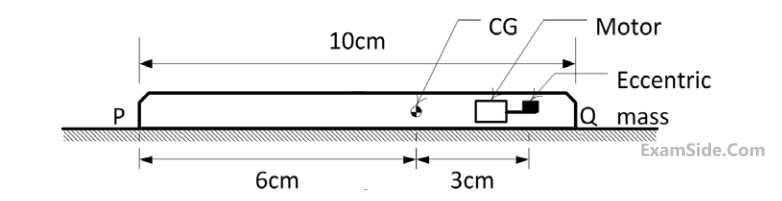

Given in addition that the eccentric mass = $$2$$ grams, eccentricity = $$2.19$$ mm, mass of the mobile = $$90$$ grams, g = $$9.81$$ $$m/{s^2}.$$ Uniform speed of the motor in $$RPM$$ for which the mobile will get just lifted off the ground at the end $$Q$$ is approximately
2
GATE ME 2015 Set 1
Numerical
+2
-0
A precision instrument package (m = 1kg) needs to be mounted on a surface vibrating at 60 Hz. It is desired that only 5% of the base surface vibration amplitude be transmitted to the instrument. Assume that the isolation is designed with its natural frequency significantly lesser than 60Hz, so that the effect of damping may be ignored. The stiffness (in N/m) of the required mounting pad is _____________.
Your input ____
3
GATE ME 2015 Set 1
MCQ (Single Correct Answer)
+2
-0.6
Considering massless rigid rod and small oscillations, the natural frequency (in rad/s) of vibration of the system shown in the figure is
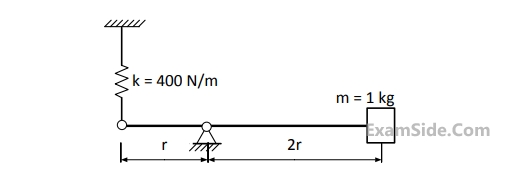

4
GATE ME 2014 Set 4
Numerical
+2
-0
A single degree of freedom system has a mass of 2kg, stiffness 8 N/m and viscous damping ratio 0.02. The dynamic magnification factor at an excitation frequency of 1.5 rad/s is ___________
Your input ____
Questions Asked from Vibrations (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ME 2025 (1)
GATE ME 2024 (1)
GATE ME 2022 Set 2 (1)
GATE ME 2022 Set 1 (1)
GATE ME 2017 Set 2 (1)
GATE ME 2017 Set 1 (1)
GATE ME 2016 Set 3 (1)
GATE ME 2016 Set 2 (1)
GATE ME 2016 Set 1 (1)
GATE ME 2015 Set 2 (1)
GATE ME 2015 Set 3 (1)
GATE ME 2015 Set 1 (3)
GATE ME 2014 Set 4 (1)
GATE ME 2014 Set 3 (2)
GATE ME 2014 Set 2 (1)
GATE ME 2014 Set 1 (2)
GATE ME 2013 (1)
GATE ME 2012 (1)
GATE ME 2011 (2)
GATE ME 2010 (1)
GATE ME 2009 (2)
GATE ME 2008 (2)
GATE ME 2007 (2)
GATE ME 2006 (3)
GATE ME 2005 (1)
GATE ME 2004 (2)
GATE ME 2003 (3)
GATE ME 2001 (1)
GATE ME 2000 (1)
GATE ME 1999 (1)
GATE ME 1996 (1)
GATE ME Subjects
Engineering Mechanics
Machine Design
Strength of Materials
Heat Transfer
Production Engineering
Industrial Engineering
Turbo Machinery
Theory of Machines
Engineering Mathematics
Fluid Mechanics
Thermodynamics
General Aptitude