1
GATE ME 2003
MCQ (Single Correct Answer)
+2
-0.6
A flexible rotor-shaft system comprises of a $$10kg$$ rotor disc placed in the middle of a mass-less shaft of diameter $$30$$ $$mm$$ and length $$500mm$$ between bearings (shaft is being taken mass-less as the equivalent mass of the shaft is included in the rotor mass) mounted at the ends. The bearings are assumed to simulate simply supported boundary conditions. The shaft is made of steel for which the value of $$E$$ is $$\,2.1\, \times \,{10^{11}}\,$$. Pa. What is the critical speed of rotation of the shaft?
2
GATE ME 2001
MCQ (Single Correct Answer)
+2
-0.6
The assembly shown in the figure is composed of two massless rods of length $$l$$ with two particles, each of mass $$m$$. The natural frequency of this assembly for small oscillations is
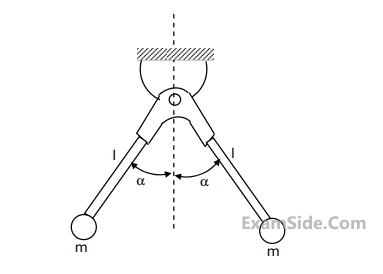

3
GATE ME 2000
MCQ (Single Correct Answer)
+2
-0.6
As shown in Figure, a mass of 100 kg is held between two springs. The natural frequency of vibration of the system, in cycles/s, is
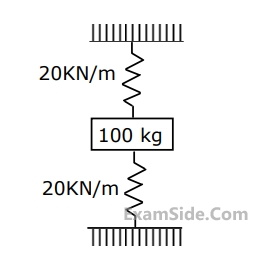

4
GATE ME 1999
MCQ (Single Correct Answer)
+2
-0.6
Consider the system of two wagons shown in Figure. The natural frequencies of this system are
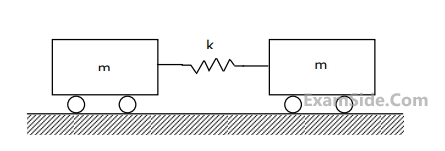

Questions Asked from Vibrations (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ME 2025 (1)
GATE ME 2024 (1)
GATE ME 2022 Set 2 (1)
GATE ME 2022 Set 1 (1)
GATE ME 2017 Set 2 (1)
GATE ME 2017 Set 1 (1)
GATE ME 2016 Set 3 (1)
GATE ME 2016 Set 2 (1)
GATE ME 2016 Set 1 (1)
GATE ME 2015 Set 2 (1)
GATE ME 2015 Set 3 (1)
GATE ME 2015 Set 1 (3)
GATE ME 2014 Set 4 (1)
GATE ME 2014 Set 3 (2)
GATE ME 2014 Set 2 (1)
GATE ME 2014 Set 1 (2)
GATE ME 2013 (1)
GATE ME 2012 (1)
GATE ME 2011 (2)
GATE ME 2010 (1)
GATE ME 2009 (2)
GATE ME 2008 (2)
GATE ME 2007 (2)
GATE ME 2006 (3)
GATE ME 2005 (1)
GATE ME 2004 (2)
GATE ME 2003 (3)
GATE ME 2001 (1)
GATE ME 2000 (1)
GATE ME 1999 (1)
GATE ME 1996 (1)
GATE ME Subjects
Engineering Mechanics
Machine Design
Strength of Materials
Heat Transfer
Production Engineering
Industrial Engineering
Turbo Machinery
Theory of Machines
Engineering Mathematics
Fluid Mechanics
Thermodynamics
General Aptitude