In a digital communication system, the overall pulse shape p(t) at the receiver before the sampler has the Fourier transform P(f). If the symbols are transmitted at the rate of 2000 symbols per second, for which of the following cases is inter symbol interference zero?

Which one of the following statements about differential pulse code modulation (DPCM) is true?

Let $$X(t)$$ be a wide sense stationary random process with the power spectral density $${S_x}\left( f \right)$$ as shown in figure (a), where $$f$$ is in Hertz $$(Hz)$$. The random process $$X(t)$$ is input to an ideal low pass filter with the frequency response $$$H\left( f \right) = \left\{ {\matrix{ {1,} & {\left| f \right| \le {1 \over 2}Hz} \cr {0,} & {\left| f \right| > {1 \over 2}Hz} \cr } } \right.$$$

As shown in Figure (b). The output of the low pass filter is $$y(t)$$.

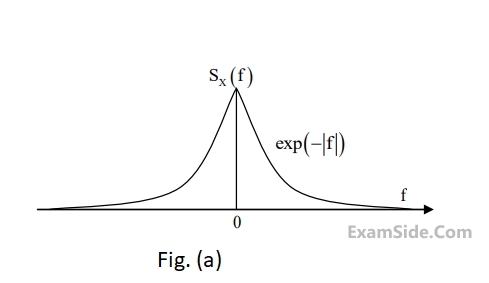
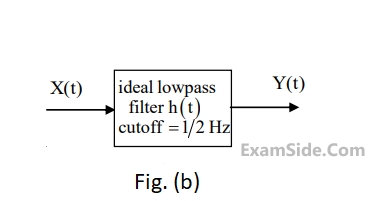
Let $$E$$ be the expectation operator and consider the following statements :
$$\left( {\rm I} \right)$$ $$E\left( {X\left( t \right)} \right) = E\left( {Y\left( t \right)} \right)$$
$$\left( {{\rm I}{\rm I}} \right)$$ $$\,\,\,\,\,\,\,\,E\left( {{X^2}\left( t \right)} \right) = E\left( {{Y^2}\left( t \right)} \right)$$
$$\left( {{\rm I}{\rm I}{\rm I}} \right)\,$$ $$\,\,\,\,\,\,E\left( {{Y^2}\left( t \right)} \right) = 2$$

Select the correct option:

In binary frequency shift keying (FSK), the given signal wave forms are
$$\,{u_o}(t) = 5\,\cos \,(20000\,\pi \,t);\,0 \le \,\,t\, \le \,T,$$ and
$${u_o}(t) = 5\,\cos \,(22000\,\pi \,t);\,0 \le \,\,t\, \le \,T,$$

where T is the bit-duration interval and t is in seconds. Both $${u_o}(t)$$ and $${u_1}(t)$$ are zero output the interval $$0 \le \,\,t\, \le \,T$$. With a matched filter (correlator ) based receiver, the smallest positive value of T (in milliseconds) required to have $${u_o}(t)$$ and $${u_1}(t)$$ uncorrelated is