Consider the Z- channel given in the figure. The input is 0 or 1 with equal probability. 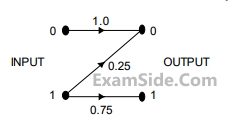If the output is 0, the probability that the input is also 0 equals____________________________________

If calls arrive at a telephone exchange such that the time of arrival of any call is independent of the time of arrival of earlier or future calls, the probability distribution function of the total number of calls in a fixed time interval will be

Consider a discrete-time channel Y = X + Z, where the additive noise Z is signal- dependent. In particular, given the trasmitted symbol $$X\, \in \,\{ \, - \,a,\,\, + \,a\} $$ at any instant, the noise sample Z is chosen independently from a Gaussian distribution with mean $$\beta X$$ and unit variance. Assume a threshold detector with zero threshold at the receiver. When $$\beta $$ = 0 the BER was found to be $$Q\,(a) = 1\, \times \,{10^{ - 8}}$$. $$\left( {Q\,\,(v)\, = {1 \over {\sqrt {2\,\pi } }}\,\int\limits_v^\infty {{e^{ - {u^2}/2}}} } \right.$$ du, and for v > 1,
use $$Q\,(v) \approx \,{e^{ - {v^2}/2}}$$
When $$\beta = - \,0.3,\,$$ the BER is closed to

Consider a communication scheme where the binary valued signal X satisfies P{X = + 1} = 0.75 and P {X = - 1} = 0.25. The received signal Y = X + Z, where Z is a Gaussian random variable with zero mean and variance $${\sigma ^2}$$. The received signal Y is fed to the threshold detector. The output of the threshold detector $${\hat X}$$ is: $$$\hat X:\left\{ {\matrix{ { + \,1,} & {Y\, > \tau } \cr { - \,1,} & {Y\, \le \,\,\tau .} \cr } } \right.$$$ To achieve a minimum probability of error $$P\{ \hat X\, \ne \,X\} $$, the threshold $$\tau $$ should be