If calls arrive at a telephone exchange such that the time of arrival of any call is independent of the time of arrival of earlier or future calls, the probability distribution function of the total number of calls in a fixed time interval will be

Consider a discrete-time channel Y = X + Z, where the additive noise Z is signal- dependent. In particular, given the trasmitted symbol $$X\, \in \,\{ \, - \,a,\,\, + \,a\} $$ at any instant, the noise sample Z is chosen independently from a Gaussian distribution with mean $$\beta X$$ and unit variance. Assume a threshold detector with zero threshold at the receiver. When $$\beta $$ = 0 the BER was found to be $$Q\,(a) = 1\, \times \,{10^{ - 8}}$$. $$\left( {Q\,\,(v)\, = {1 \over {\sqrt {2\,\pi } }}\,\int\limits_v^\infty {{e^{ - {u^2}/2}}} } \right.$$ du, and for v > 1,
use $$Q\,(v) \approx \,{e^{ - {v^2}/2}}$$
When $$\beta = - \,0.3,\,$$ the BER is closed to

Consider a communication scheme where the binary valued signal X satisfies P{X = + 1} = 0.75 and P {X = - 1} = 0.25. The received signal Y = X + Z, where Z is a Gaussian random variable with zero mean and variance $${\sigma ^2}$$. The received signal Y is fed to the threshold detector. The output of the threshold detector $${\hat X}$$ is: $$$\hat X:\left\{ {\matrix{ { + \,1,} & {Y\, > \tau } \cr { - \,1,} & {Y\, \le \,\,\tau .} \cr } } \right.$$$ To achieve a minimum probability of error $$P\{ \hat X\, \ne \,X\} $$, the threshold $$\tau $$ should be

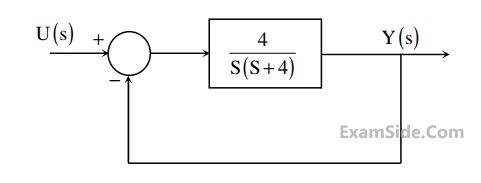
For the second order closed-loop system shown in the figure, the natural frequency (in rad/s) is