Consider a linear array of two half - wave dipoles A and B as shown in Fig. The dipoles are $${\lambda \over 4}$$ apart and are excited in such a way that the current on element B lags that on element A by $${90^0}$$ in phase

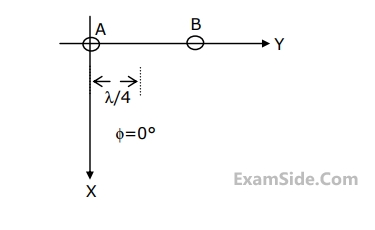
(a) Obtain the expression for the radiation pattern for E in the XY plane, i.e.,$$\left( {\theta = {{90}^0}} \right)$$.
(b) Sketch the radiation pattern obtained in (a).

The line-of-sight communication requires the transmit and receive antennas to face each other. If the transmit antenna is vertically polarized for best reception the receiver antenna should be

Consider a parallel plate waveguide with plate separation d as shown in Fig. The electric and magnetic fields for the TEM mode are given by $${E_x} = \,{E_0}\,\,{e^{ - j\,k\,z + j\,\omega \,t}},\,{H_y} = {{{E_0}} \over \eta }\,{e^{ - j\,k\,z + j\,\omega \,t}}$$

Where $$k = \,\,\eta \,\omega \,\, \in $$
(a) Determine the surface charge densities $${\rho _s}$$ on the plates at x = 0 and x = d
(b) Determine the surface current densities $$\mathop {{J_s}}\limits^ \to $$ on the same plates.
(c) Prove that $${\rho _s}$$ and $$\mathop {{J_s}}\limits^ \to $$ satisfy the current continuity condition.

Consider a parallel plate waveguide with plate separation d as shown in Fig. The electric and magnetic fields for the TEM mode are given by $${E_x} = \,{E_0}\,\,{e^{ - j\,k\,z + j\,\omega \,t}},\,{H_y} = {{{E_0}} \over \eta }\,{e^{ - j\,k\,z + j\,\omega \,t}}$$

Where $$k = \,\,\eta \,\omega \,\, \in $$
(a) Determine the surface charge densities $${\rho _s}$$ on the plates at x = 0 and x = d
(b) Determine the surface current densities $$\mathop {{J_s}}\limits^ \to $$ on the same plates.
(c) Prove that $${\rho _s}$$ and $$\mathop {{J_s}}\limits^ \to $$ satisfy the current continuity condition.