1
GATE ECE 2002
Subjective
+5
-0
The Nyquist plot of an all-pole second order open-loop system is shown in Figure.
Obtain the transfer function of the system.
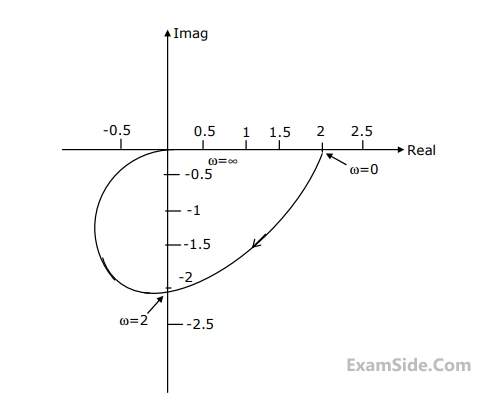

2
GATE ECE 2002
Subjective
+5
-0
A unity feedback system has the plant transfer function
Gp(s)=$${1 \over {\left( {s + 1} \right)\left( {2s + 1} \right)}}$$
(a) Determine the frequency at which the plant has a phase lah of 90o.
(b) An intergral controller with transfer function Gc(s)=$${k \over s}$$ , isplaced in the forwardpath the value of k such that the compensated system has an open loop gain margin of 2.5.
(c) Determine the steady state errors of the compensated system to unit-step and unit-ramp inputs.
(a) Determine the frequency at which the plant has a phase lah of 90o.
(b) An intergral controller with transfer function Gc(s)=$${k \over s}$$ , isplaced in the forwardpath the value of k such that the compensated system has an open loop gain margin of 2.5.
(c) Determine the steady state errors of the compensated system to unit-step and unit-ramp inputs.
3
GATE ECE 2002
MCQ (Single Correct Answer)
+1
-0.3
The transfer function Y(s)/U(s) of a system described by the state equations
$$\mathop x\limits^ \bullet $$(t) = -2x(t)+2u(t)
y(t) = 0.5x(t) is
$$\mathop x\limits^ \bullet $$(t) = -2x(t)+2u(t)
y(t) = 0.5x(t) is
4
GATE ECE 2002
Subjective
+5
-0
The block diagram of a linear time invariant system is given in Figure is
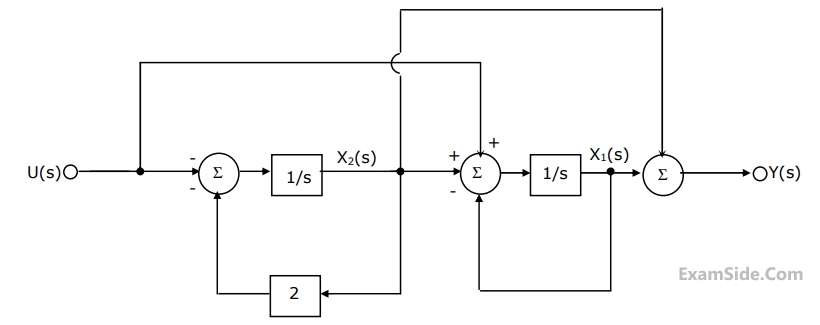 (a) Write down the state variable equations for the system in matrix form
assuming the state vector to be $${\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right)} \right]^T}$$
(a) Write down the state variable equations for the system in matrix form
assuming the state vector to be $${\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right)} \right]^T}$$
(b) Find out the state transition matrix.
(c) Determine y(t), t ≥ 0, when the initial values of the state at time t = 0 are $${x_1}$$(0) = 1, and $${x_2}$$(0) = 1.
 (a) Write down the state variable equations for the system in matrix form
assuming the state vector to be $${\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right)} \right]^T}$$
(a) Write down the state variable equations for the system in matrix form
assuming the state vector to be $${\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right)} \right]^T}$$
(b) Find out the state transition matrix.
(c) Determine y(t), t ≥ 0, when the initial values of the state at time t = 0 are $${x_1}$$(0) = 1, and $${x_2}$$(0) = 1.
Paper analysis
Total Questions
Analog Circuits
4
Communications
3
Control Systems
11
Digital Circuits
7
Electromagnetics
11
Electronic Devices and VLSI
4
Microprocessors
2
Network Theory
8
Signals and Systems
10
More papers of GATE ECE
GATE ECE 2025
GATE ECE 2024
GATE ECE 2023
GATE ECE 2022
GATE ECE 2021
GATE ECE 2019
GATE ECE 2018
GATE ECE 2017 Set 2
GATE ECE 2017 Set 1
GATE ECE 2016 Set 3
GATE ECE 2016 Set 2
GATE ECE 2016 Set 1
GATE ECE 2015 Set 2
GATE ECE 2015 Set 3
GATE ECE 2015 Set 1
GATE ECE 2014 Set 1
GATE ECE 2014 Set 4
GATE ECE 2014 Set 3
GATE ECE 2014 Set 2
GATE ECE 2013
GATE ECE 2012
GATE ECE 2011
GATE ECE 2010
GATE ECE 2009
GATE ECE 2008
GATE ECE 2007
GATE ECE 2006
GATE ECE 2005
GATE ECE 2004
GATE ECE 2003
GATE ECE 2002
GATE ECE 2001
GATE ECE 2000
GATE ECE 1999
GATE ECE 1998
GATE ECE 1997
GATE ECE 1996
GATE ECE 1995
GATE ECE 1994
GATE ECE 1993
GATE ECE 1992
GATE ECE 1991
GATE ECE 1990
GATE ECE 1989
GATE ECE 1988
GATE ECE 1987
GATE ECE
Papers
2025
2024
2023
2022
2021
2019
2018
2014
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987